CMU 15-445/645 Lecture 7: Trees Indexes I

表索引是表属性子集中的一个副本,负责组织和排序,通过这些属性,可以更有效地访问。DBMS 需要确保表中的内容和索引在逻辑同步。

DBMS 工作之一就是要找出最佳的索引去执行每一次查询。在实际情况中,索引的数量经常需要做出取舍,如果索引数量过多会有:
存储数据过大:索引往往需要额外的存储空间
维护成本过高:更新数据时候索引也要被更新

在表索引中经常使用的数据结构是 B-Tree,B-Tree 既指的是平衡树一族的数据结构,也是它们当中的一个数据结构,B-Tree 一族包括:
B-Tree(1971)
B+Tree(1973)
B*Tree(1977)
B-Link-Tree(1981)

B+Tree 是自平衡树,总是保持数据的有序性,方便查找和顺序访问,插入和删除的时间复杂度都是 O(log n)。
二分查找树的更通用形式,node 上可以拥有两个以上的节点
为大量读取读写数据的系统进行了优化
虽然这种数据结构是为了慢速硬盘和内存设计的数据结构,但是即使放在现在有更快的硬件加持下,也是最好的选择之一。

B+Tree 是一棵多路查找树,意味着它一个叶子节点可以被多条路径找到,拥有如下性质:
完美的平衡(例如,叶子节点总是保持一样的高度)
除了根节点外,至少要保持半满状态,M/2-1 <= #key <= M-1
每个内部节点有 k 个 key,就会有 k+1 个非空子节点
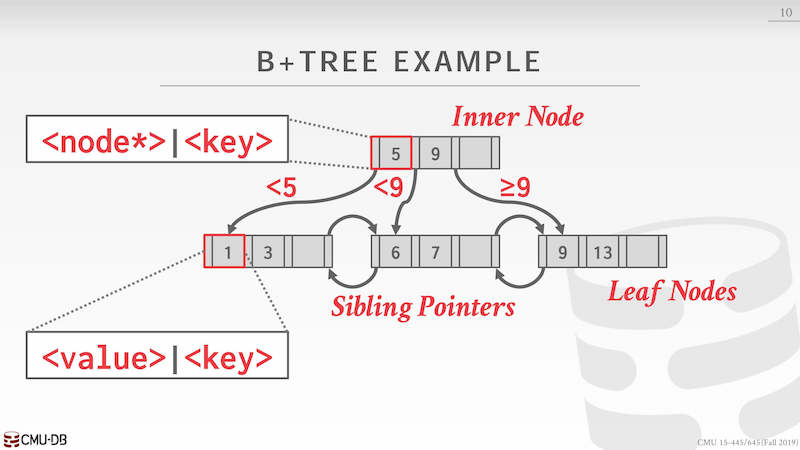
在 B+ Tree 中节点分为 inner node、leaf node,leadf nodes 使用双向链表链接。inner node 结构为 <node*> | ,这里的 node 指针指向下一层的 node,如果没有可能是 null;leaf node 结构与 inner node 不同,组织形式为 | ,value 可以是具体的值也可以是某些 ID。

B+ 树 node 本质就是一个 kv 对组成的数组,value 在 inner node 和 leaf node 上有不同的表现形式,node 组成的数组经常按照有序的方式排列,方便顺序查找。
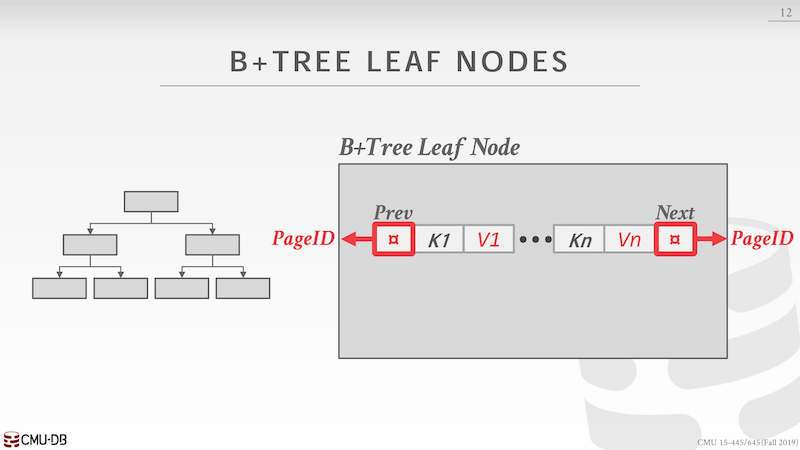
这是教科书中方式,实际上在数据库中不会这样存储
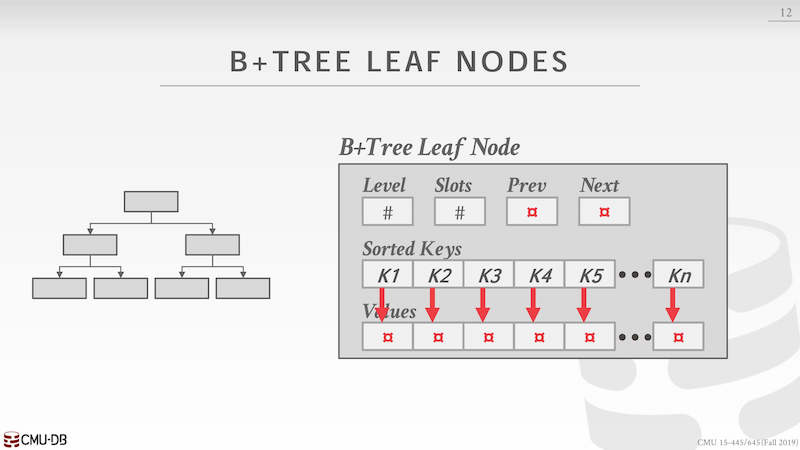
在 leaf node 中除了记录下一些属性用作快速判断以外,key 和 value 通常是分开存储。当进行二分查找时候 value 并不参与,如果组合在一起存储就有浪费。key 是定长或者变长,与 value 分离可以更好进行二分查找,value 通常是定长的,key 中有对应 value 的 offset 值。因此只需要拿到 key 就能跳转到 value 的 offset 处,拿到想要的值。

Value 的存储方式一般来说有两种,存储指向数据的指针或者就是数据本身

与原始的 B-Tree 可以把 value 存在任意节点上,但是 B+Tree 只能存储在 leaf node 上。
B-Tree 中的 key 只会出现一次,B+Tree 中 inner node 存查找路径,可能会有重复。
删除 B+Tree leaf node 中的 key,inner node 中的 key 还可能存在
相比之下 B-Tree 不会有重复的 key 更节省空间,但是在多线程操作下 key 可能要向上或者向下移动。而 B+Tree 只对 leaf node 操作,同时只有向上的操作

B+ Tree 插入操作:
找到要插入的 leaf node L
按照顺序添加数据记录到 L
- 如果 L 没有足够的空间
- 分裂 L 成 L 和 L2
- 平均分配数据到 L 和 L2 中
- 找出它们中间的 key,放入父节点
- 如果 L 没有足够的空间

B+ Tree 删除操作:
在 leaf node 中找到要删除的 key
删除以后如果无法保持半满状态,需要重新分配
- 从相同父节点的兄弟姐节点中拿
- 如果无法拿到就需要合并 node
如果触发了合并,需要在 L 的父节点中删除记录

一般填充系数为 67% ~ 69%,意味着所有保存的数据中只有这部分才有用。
如何计算 B+ Tree 做多存多少条数据?
假设一个 page 是 8K,每条记录 key 的大小为 4B,指针 6B
每页可以存放 8 * 1024 / (4+6) = 819 个索引
两层一共可以存 819 * 8 = 6553,三层一共可以存 819 * 819 * 8 = 5366907,四层一共可以存 819 * 819 * 819 * 8 = 4395496833

表中的数据是通过 primary key 来组织有序,可以是 heap 或者 index。一些数据库会总是使用 clustered indexes ,如果没有会自动生成一个,有一些数据库可能不使用。

当我们采用 B+ Tree 索引来查询的时候可以只使用 key 中的部分属性。比如 index 是 <a,b,c> 可以支持 a=5 AND b=3,也支持 b=3;然而对于 hash index 而言,必须要提供全部的 key 属性才能找到。
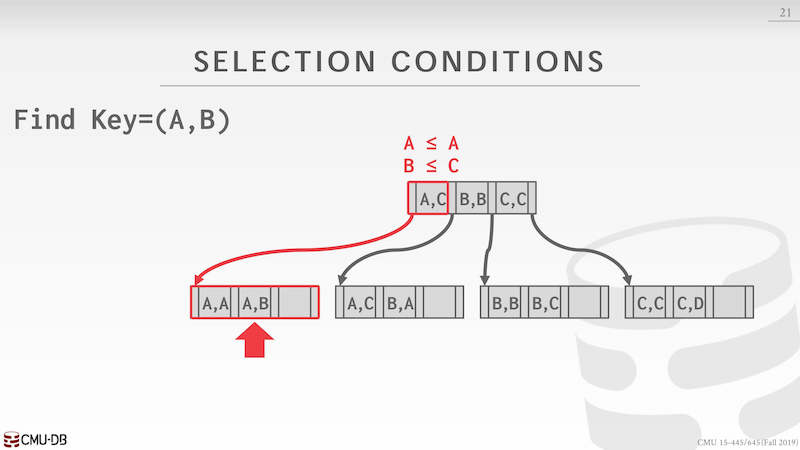
第一情况是给定了索引的 key=(A,B),可以对比索引发现 A <= A,B <= C 就定位到第一个 leaf node。
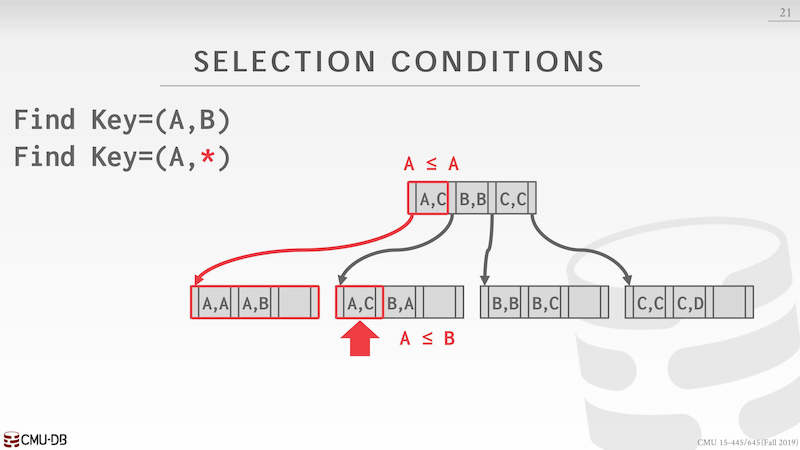
第二种情况复杂一些 key=(A,*) 通过对比第一个属性发现了两个 leaf node,在第二个 leaf node 中发现了 B,A 不满足条件,就可以停止查询。
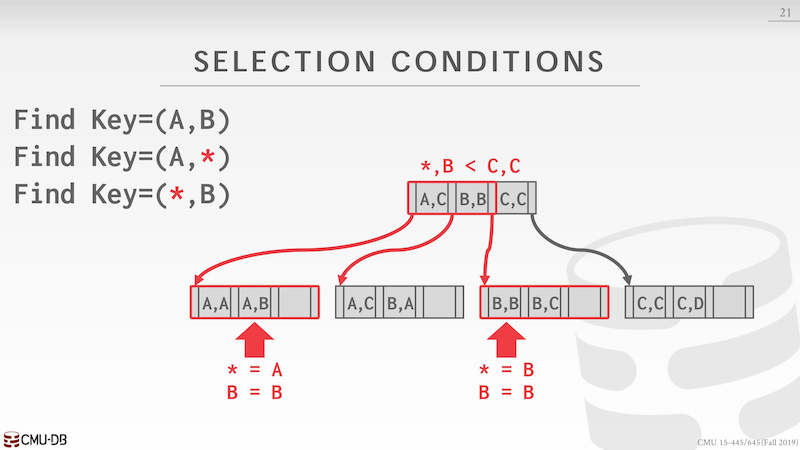
第三种情况 key=(*,B) 对于这种情况,需要把所有的可能值带入 *,进行多次查找后在组合数据,这当中方式效率最低。

我们可以把一个 node 当成一个 page 来分析,对于 HDD 来说 1MB,SSD 10KB、Memory 512B。node 的 size 取决了有多少随机 IO 和顺序 IO,也就是扫描时候的速度。对于越快的设备随机 IO 更快,扫描的大小也越小;慢速设备更大的 size 可以减小随机 IO,相比扫描范围也变大。

合并 node 的代价比较高昂,所以并不是每次都会触发合并操作。往往都是把多个的 merge 操作延后执行,或者选择在某个时候整体重建。

可变长的 key 目前大致有这 4 种方案:
存储指针指向真正的数据:这种方式代价比较高,基本没人用
可变的 size 的 node:不能很好的进行内存管理,固定大小 buffer pool 更有优势
填充大小:总是填充空值到最大长度,空间浪费严重
间接 key map:在 node 内的一个指针数组,指针指向 key value 组成的 list
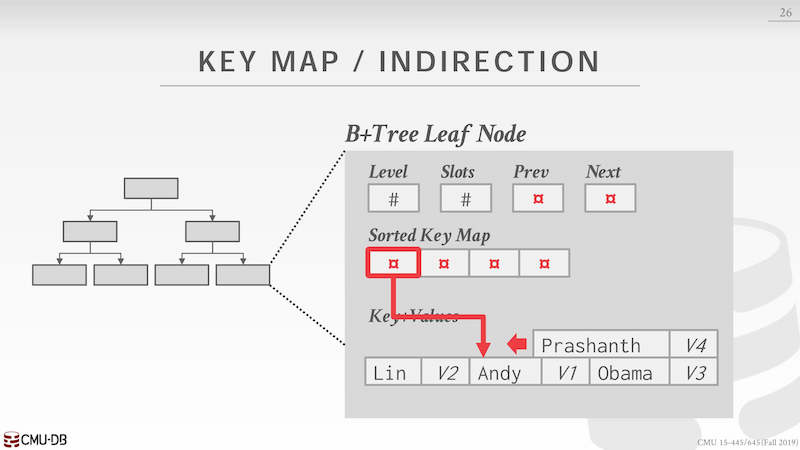
Sorted Key Map 数组本质上存储的是 key value list 的 offset。当对数组排序的时候并不需要真实的挪动数据,只需要根据 offset 指向的 key 排序 offset 即可。

非唯一索引 key 和 value 都可能是多个,存储是方式有重复 key 和 value 列表
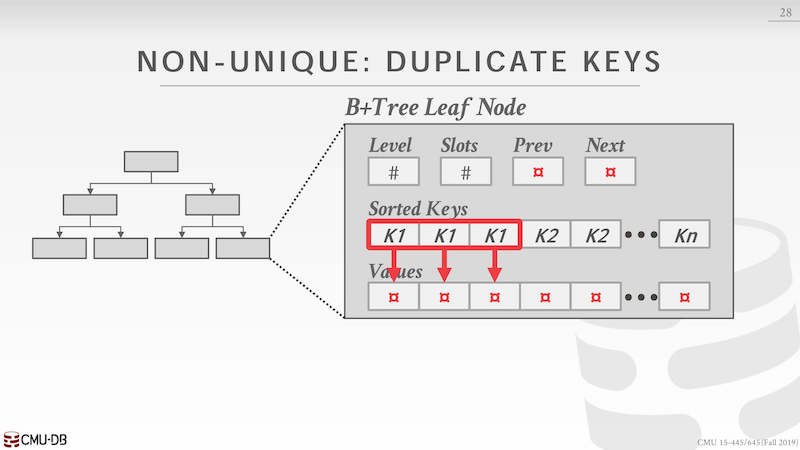
重复 key,需要考虑一样的 key 会被存在多个 leaf node 上,每一个 key 对应自己的 value
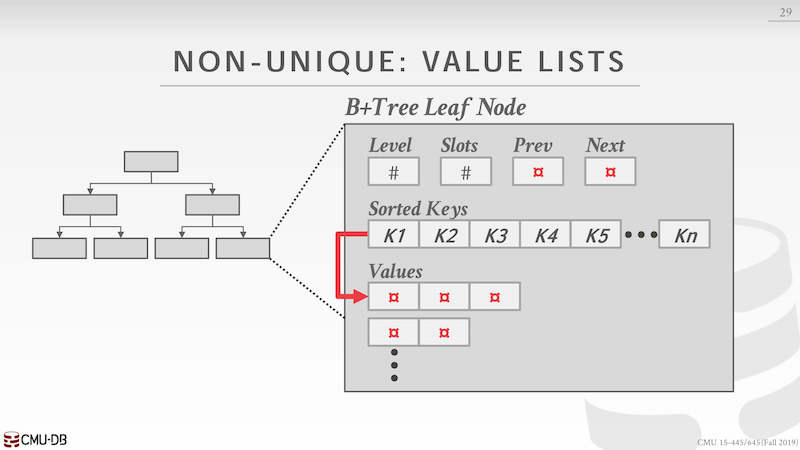
value 列表,key 只有一个但是 value 会有多个

在一个 node 中查找到一个 key 有三种方法:
线性搜索,不需要维护有序性
二分查找,需要时时刻刻维护有序性
差值搜索,需要事先收集 key 的分布信息
二分搜索是最常见的方式

存在同一个 leaf node 上的数据都是有序的,它们往往有相同的前缀,使用前缀压缩可以减少空间。
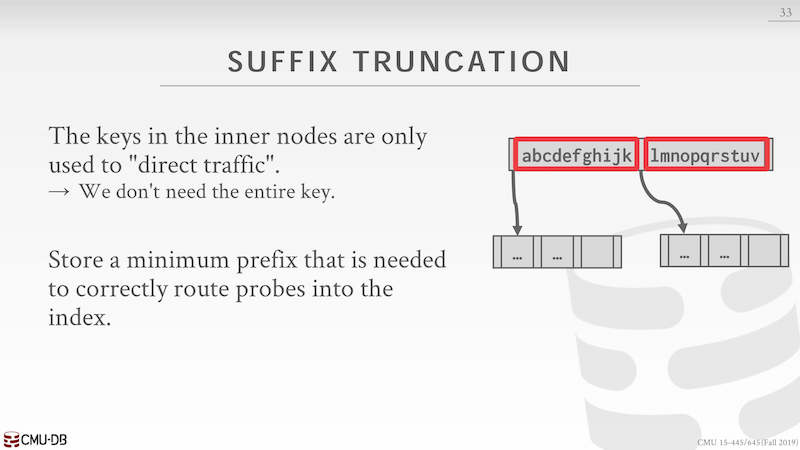
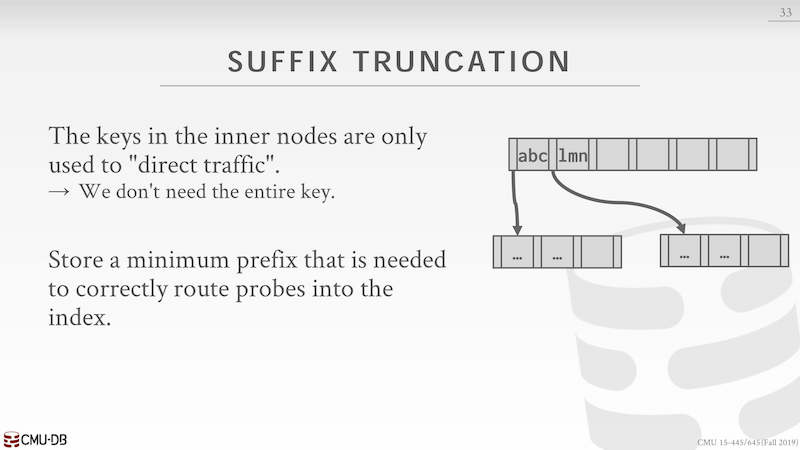
后缀截断,在 key 的查找过程中只需要前面几个字符就能判断出 key 的走向,所以只不需要存储完整的 key。
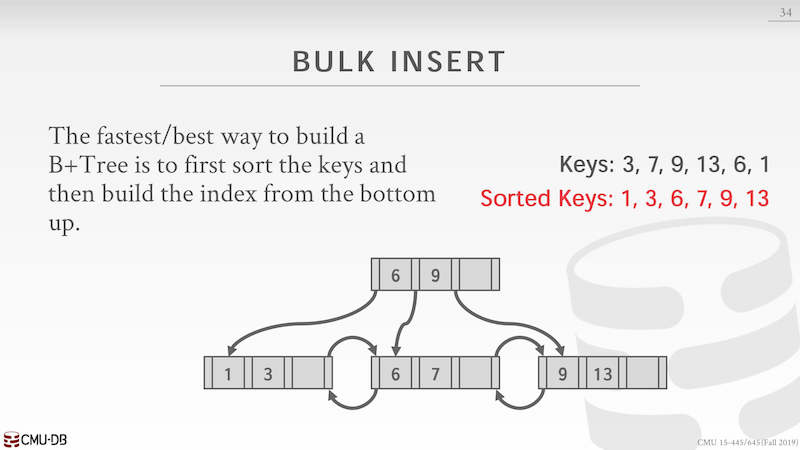
Bulk insert 可以不通过自上而下的插入数据,可以自下而上先构建好 B+ Tree 然后与原来的进行一次 Merge。

node 中使用 page id 来存储下一个想要的 page,比如上层到下层,或者 leaf node 的兄弟 page。一般来说流程是:发现 page id,到 buffer pool 中根据 page id 找到 page 的内存地址返给 B+Tree。
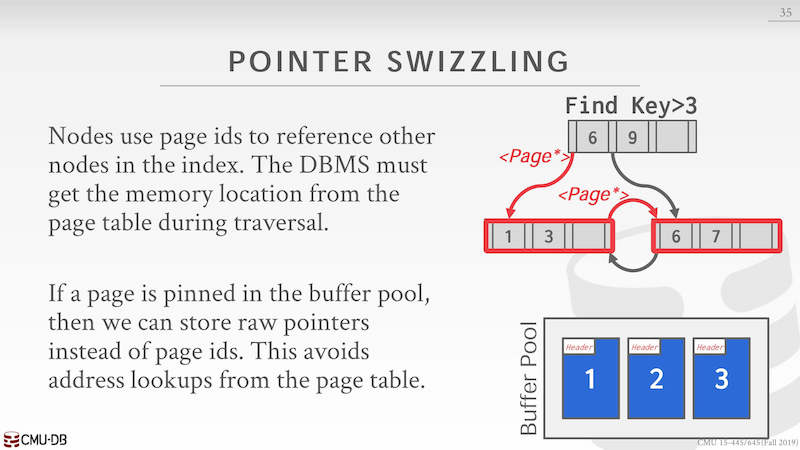
但是对于比较接近 root node 的那些 inner node,它们被访问的频率很高,同时一个 page 被刷入磁盘后再加载回来的内存地址是会变化。所以对于高频率访问的 page 可以直接固定在 buffer pool 中,当寻找这些 page 时候不再使用 page 而是直接使用内存地址。