正小歪 BLOG

CMU 15-445/645 Lecture 6: Hash Tables

设计目标：

  • 数据组织（Data Organization）：如何在内存或者 pages 中排布数据，需要存储什么信息可以支持高效的防访问
  • 并发（Concurrrency）：如何确保在同一时间多线程的访问不会出现问题

Hash Table 实现了一个无序的关联数组来存储 key 和 value，使用 Hash 函数计算出要插入 key 的 offset，以此来找到要存储的 value。

  • 空间复杂度：O(n)
  • 操作复杂度：
    • 平均：O(1)
    • 最坏：O(n)

申请一个数组，每个元素都可以存储一个 key，通过 hash 计算出在数组中的 offset，数组中存储着指向 value 的指针。这里有一些必须要满足的假设：

  1. 每一个 key 都是唯一
  2. 不同的 key 存在不同的 hash 值

所以 Hash Table 的设计目标就有：

  1. Hash Function：如何把一个 key 转化成一小段空间，一般是固定的 32 bit 或者 64 bit 的整数；在速度和碰撞率上做出取舍，更快意味着会出现更多冲突
  2. Hash Schema：如何处理 hash 后 key 发生了冲突；在空间和处理 key 的方法上做取舍，如果空间很大 key 的冲突概率就很小，反之如果空间很小就需要有额外的方法处理 key

Hash Function

输入任意的 key 返回一个整型的数字，在 DBMS 并不使用加密的 hash 函数，更关心的是更快速度和更低的碰撞率。

  • CRC-64 (1975) → Used in networking for error detection.

  • MurmurHash (2008) → Designed to a fast, general purpose hash function.

  • Google CityHash (2011) → Designed to be faster for short keys (<64 bytes).

  • Facebook XXHash (2012) → From the creator of zstd compression.

  • Google FarmHash (2014) → Newer version of CityHash with better collision rates.

综合素质来看 XXHash 相比其他 hash 函数拥有更快的速度和更低碰撞率，XXHash 有最新的 XXHash3 版本应该在数据库系统中优先使用。

Static Hasing Schemes

静态 hash 都需要在使用前需要提前知道希望保存 key 的数量，当存满的时候需要扩容这时候会把第一个 hash table 中所有的 key 拷贝到新的 hash table 中，一般这么做代价很高

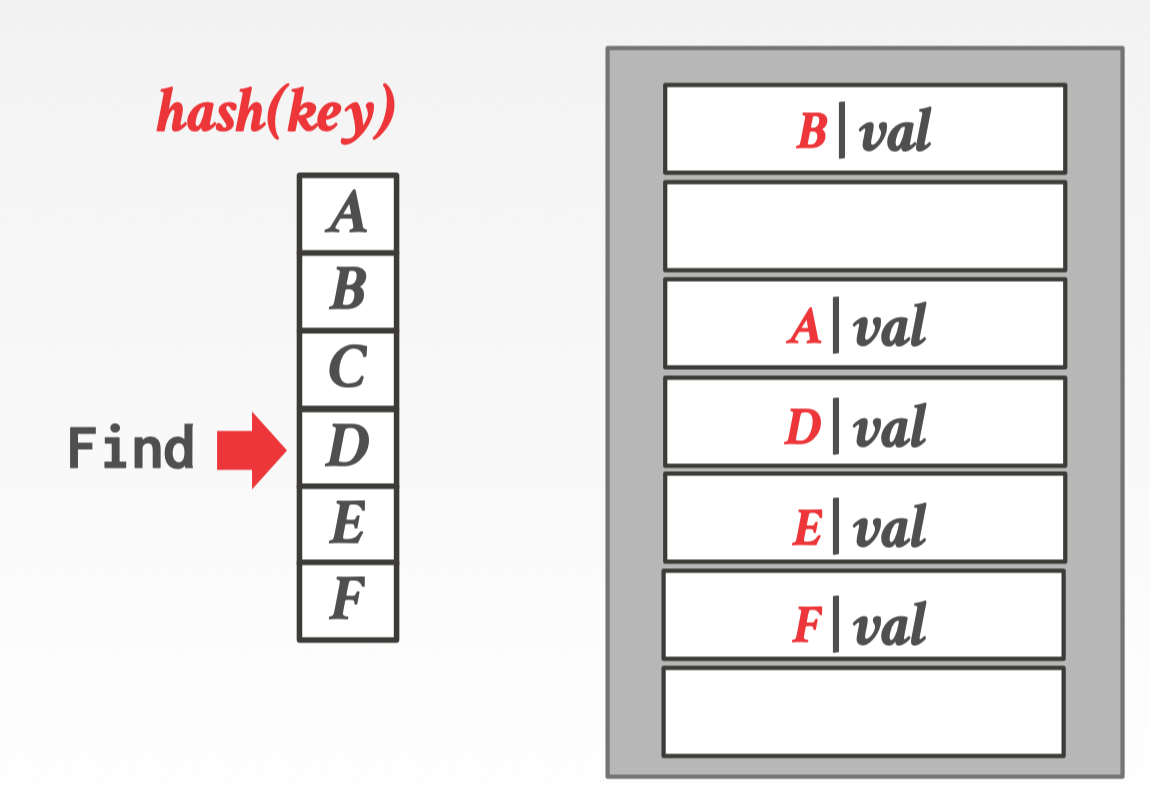
Linear Probe Hashing

解决碰撞的方式就是在 table 中寻找下一个空闲的 slot

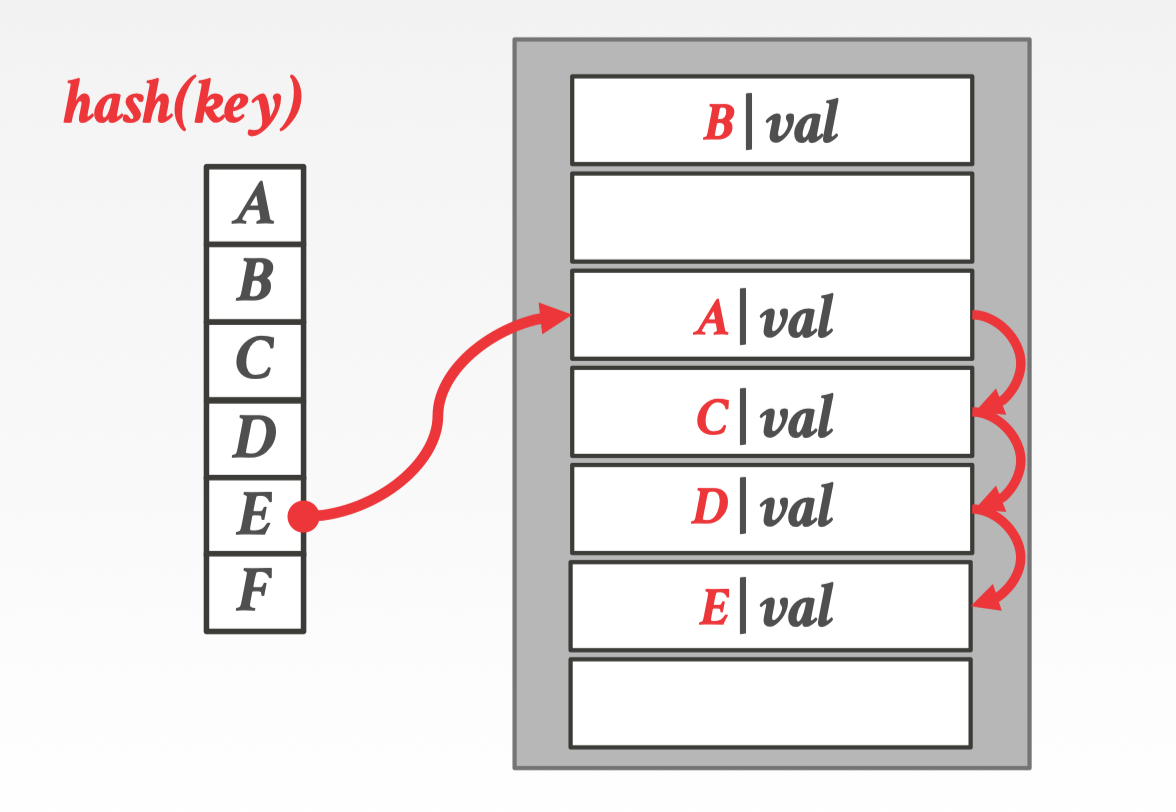
image-20230425085119563

图中 hash(E) 后发现自己位置上已经存在了 A 就沿着顺序往下找直到发现 D 后面有一个空闲的 slot

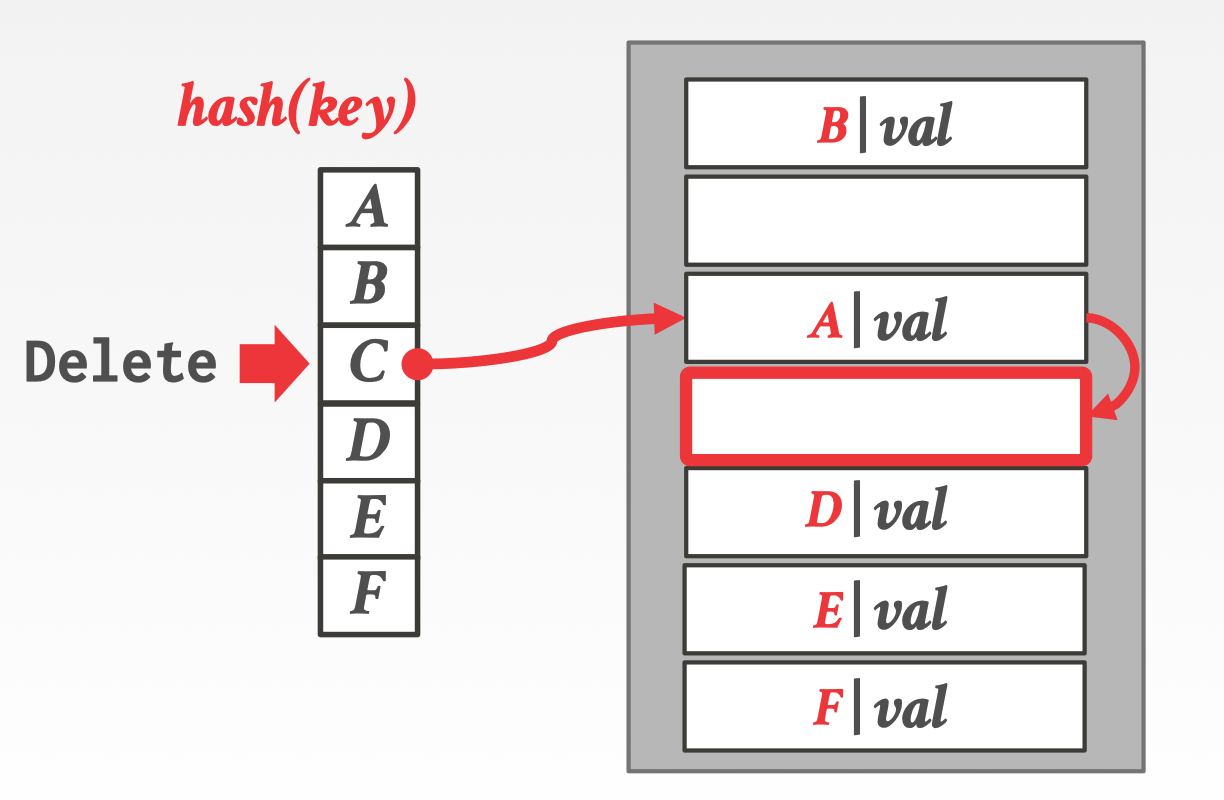
image-20230425085326812

删除时候后同理，先找到了 A 的位置然后向下搜索匹配，发现 C 后删除

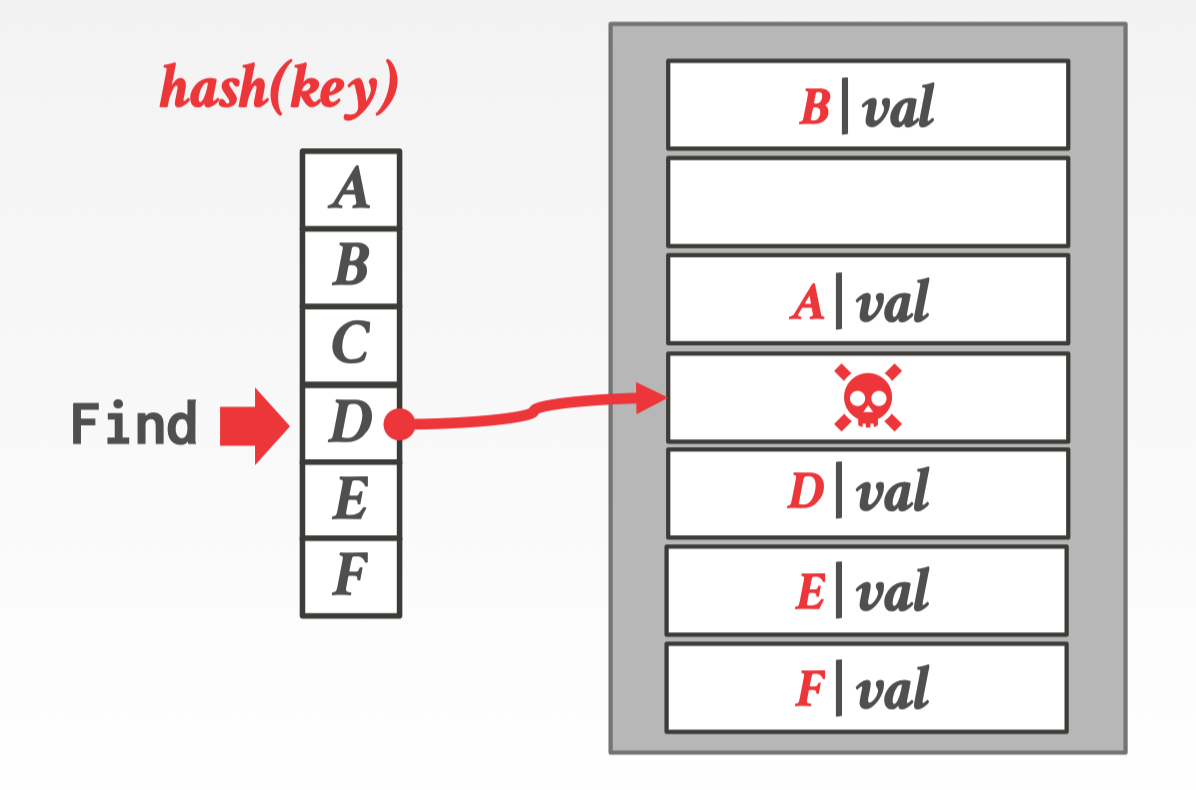
image-20230425085502765

删除之后就出现了空洞，如果空洞存在下次在 Find(D) 时候定位了空洞会就会发现没有找到。是因为 D 的插入是由于 C 存在向下找到空 slot 后插入的，所以 D 的位置是根据 C 的位置的 offset 来决定。一旦 C 被删除造成了空洞，D 也随之无法找到。

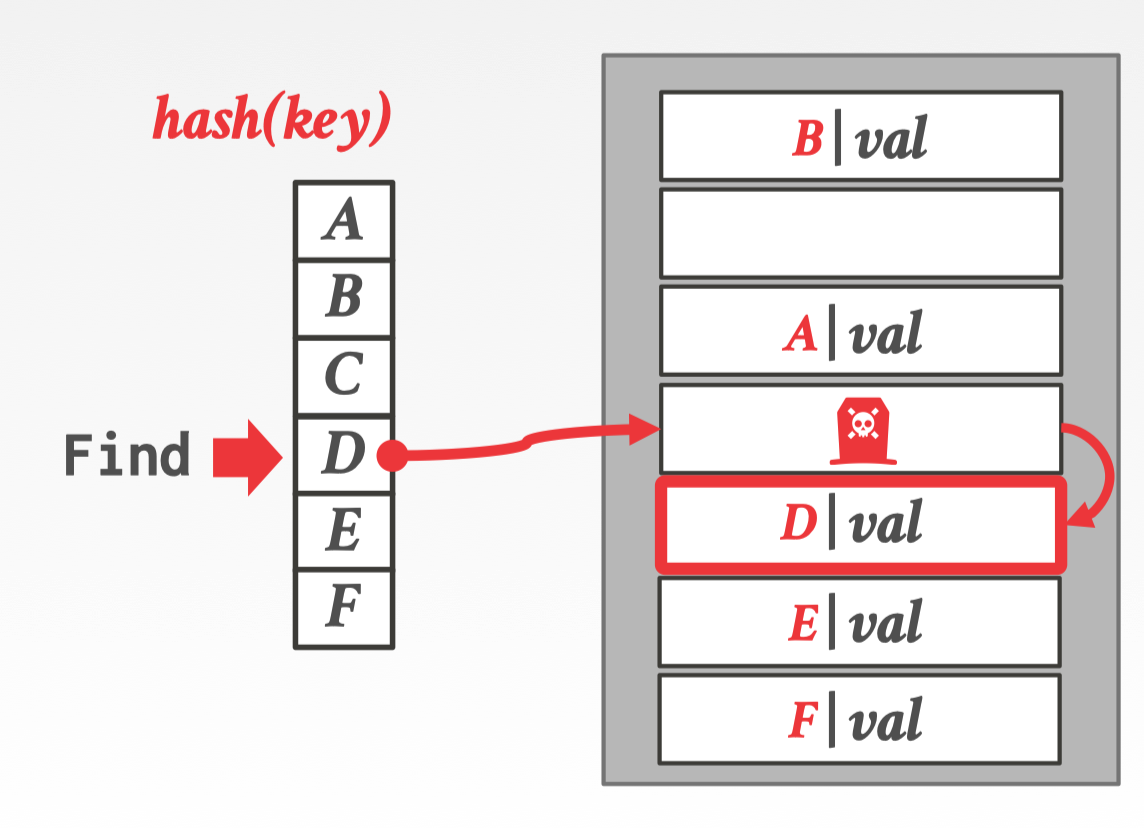
image-20230425085837987

解决的方法之一就是采用墓碑机制，删除并不是真正删除，只是标记成墓碑。这使得在 Find(D) 的时候仍然可以发现这个 slot 被占用了然后接着向下寻找。

image-20230425090004112

另一种方式就是通过移动来填补空洞，既然 C 的位置已经被删除，那么把 D 及其以下的 slot 都往上移动，补齐空洞。

在实际中，更多采用的是墓碑机制而不是移动。移动虽然更可以更快的回收 slot 但是带来的问题也更多，移动 slot 需要花费更多的时间，而且移动时候也需要考虑环形 slot 头尾节点问题。

image-20230425091230610

在 hash table 中比如作为 primary index 的 key 是唯一的，但是有时候 key 也不一定是唯一。这时候一般有两种处理方式，一种是给每个 key 都保留一个 value list，第二种是存储冗余的 key 和 value。明显看出第二种方式会使用更多空间，因为 key 需要存储多份，但是在实际情况下第二种方式用的也会更多，因为更简单。

Robin Hood Hashing

线性 Hash 的一个变种，可以偷取 “富有” 的 Key 的 Slot 分给 “贫穷” 的 Key。

  • 每个 Key 跟踪自己与原有位置之间的 offset，offset 越大表示越 “贫穷”
  • 当插入一个 Key 时候，如果第一个 Key 的 offset 比 第二个 Key 的 offset 更小，第一个 Key 的 Slot 会被占用

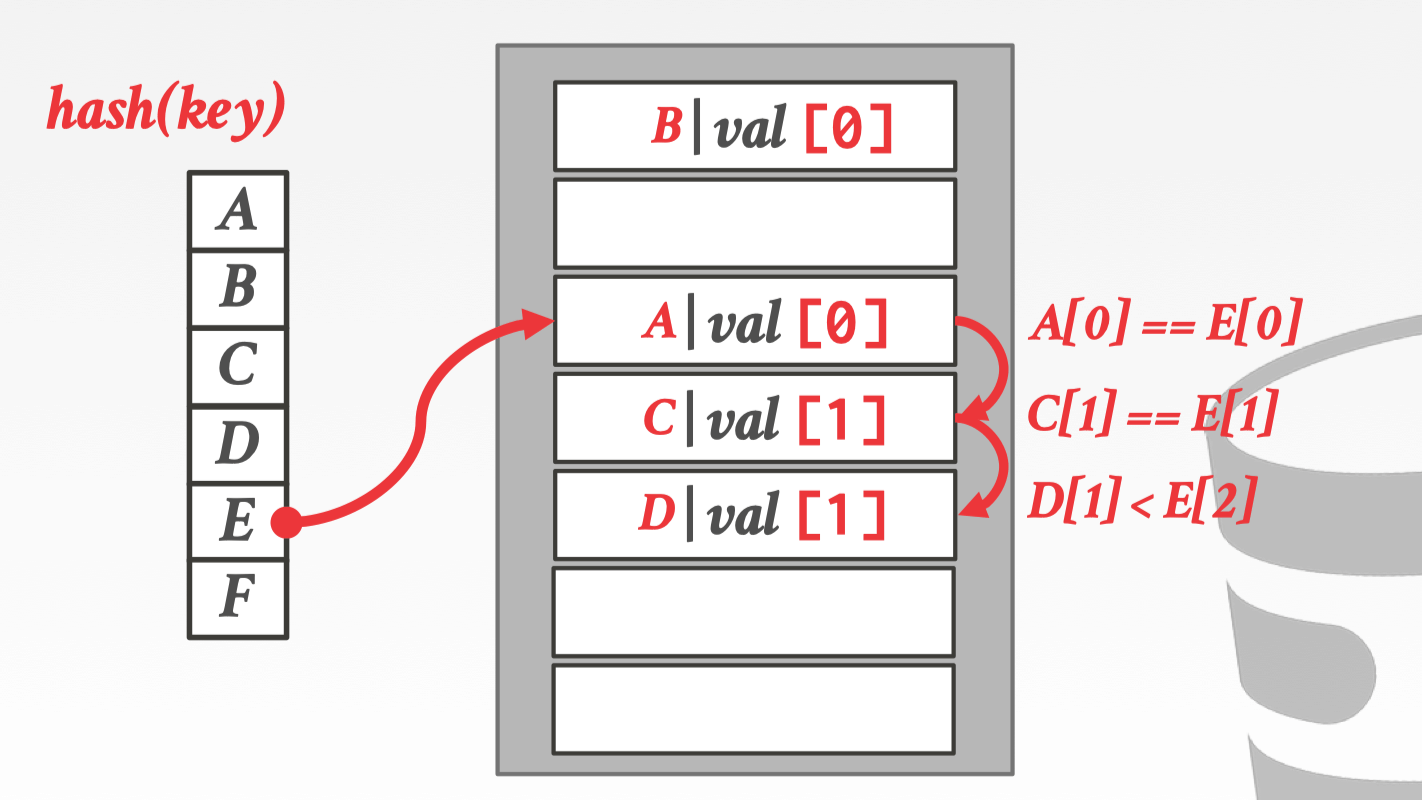
当插入 E 的时候，原本的 slot 中已经有一个 A，对比 A 的 offset 与自己的 offset 都是 0，不能占用。接着往下对比 C 发现 offset 都是 1，也不能占用。往下对比 D，此时 D 的 offset 是 1，E 的 offset 是 2，所以此时的 E 比 D 更 “贫穷”，可以占用 D 的位置。

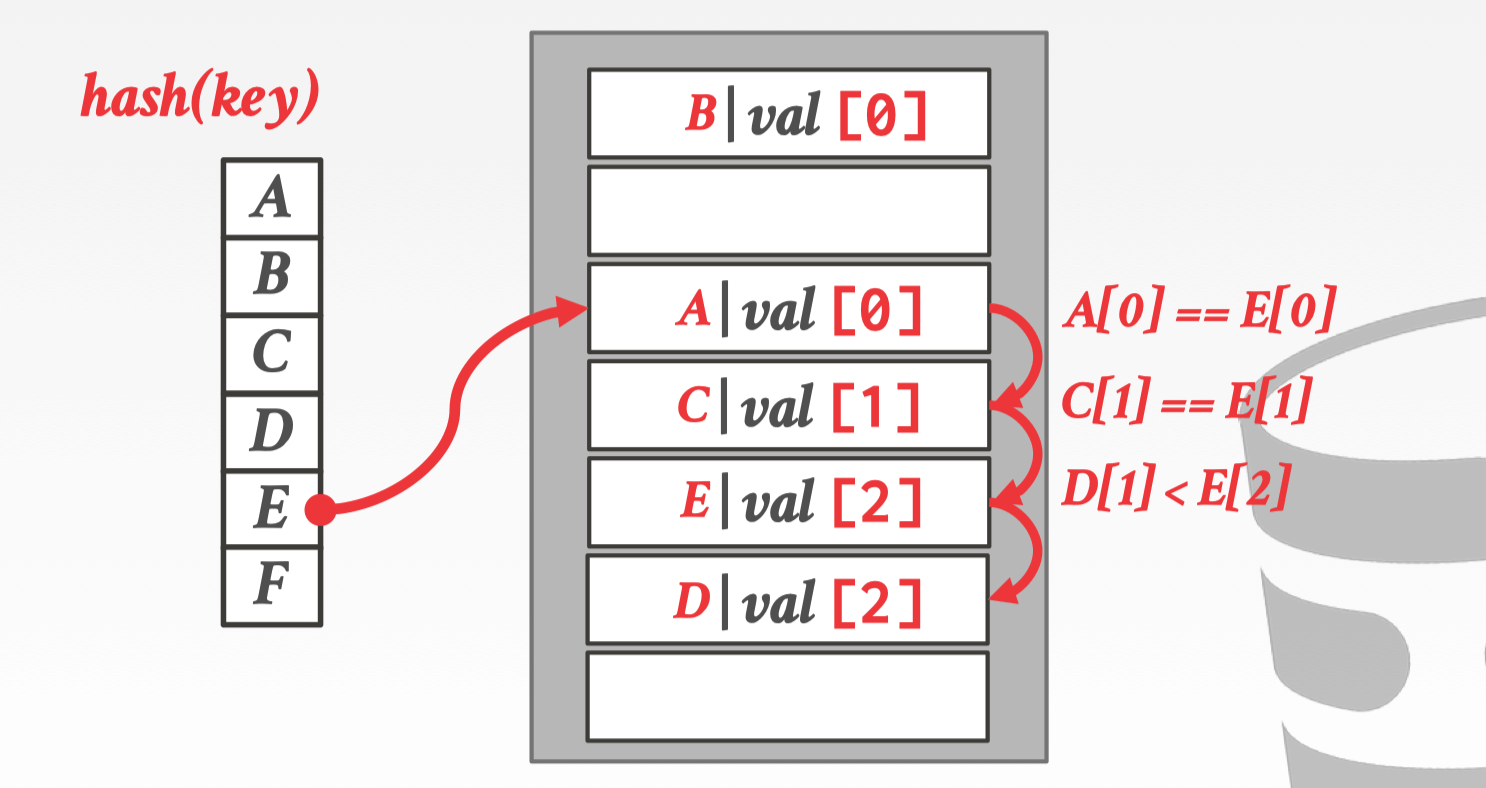
E 把 D 的 slot 占用以后，D 继续往下寻找位置，发现是一个空的 Slot，便可以插入，此时 D 的 offset 变为 2。

Cuckoo Hashing

使用多个不同 Seed 的 Hash Table，一般在生产环境中是 2 个。

  • 当插入时候，检查每个 table 哪里有空闲的 slot
  • 如果 table 没有空闲的 slot，逐出当前位置中的 key，重新 hash 到另一个位置

查找的时间复杂度总是 O(1) 因为每个位置只 hash table 中检查一次。

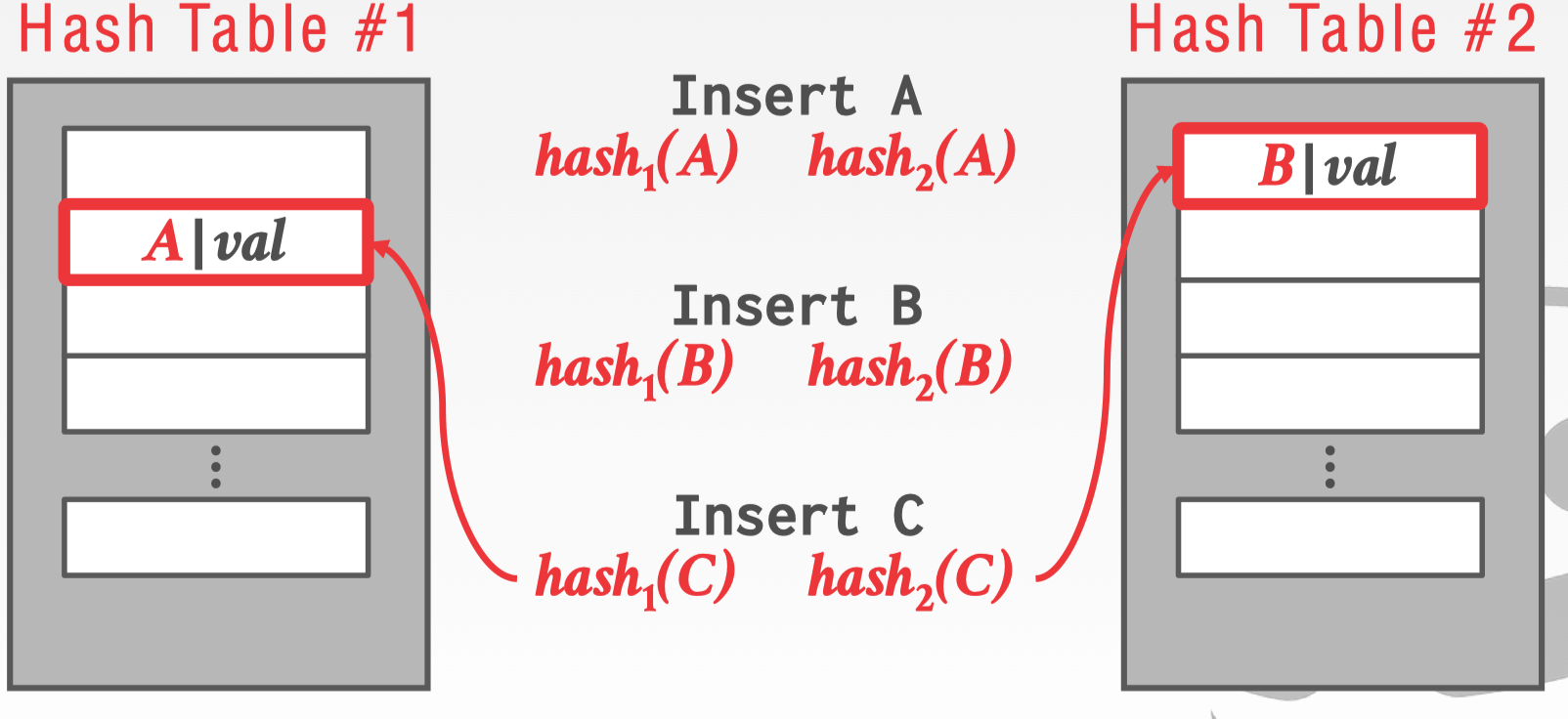
当 Insert C 的时候发现两个 Hash Table 都没有可有插入 slot，假设此时占用 B 的位置，B 就会被逐出。

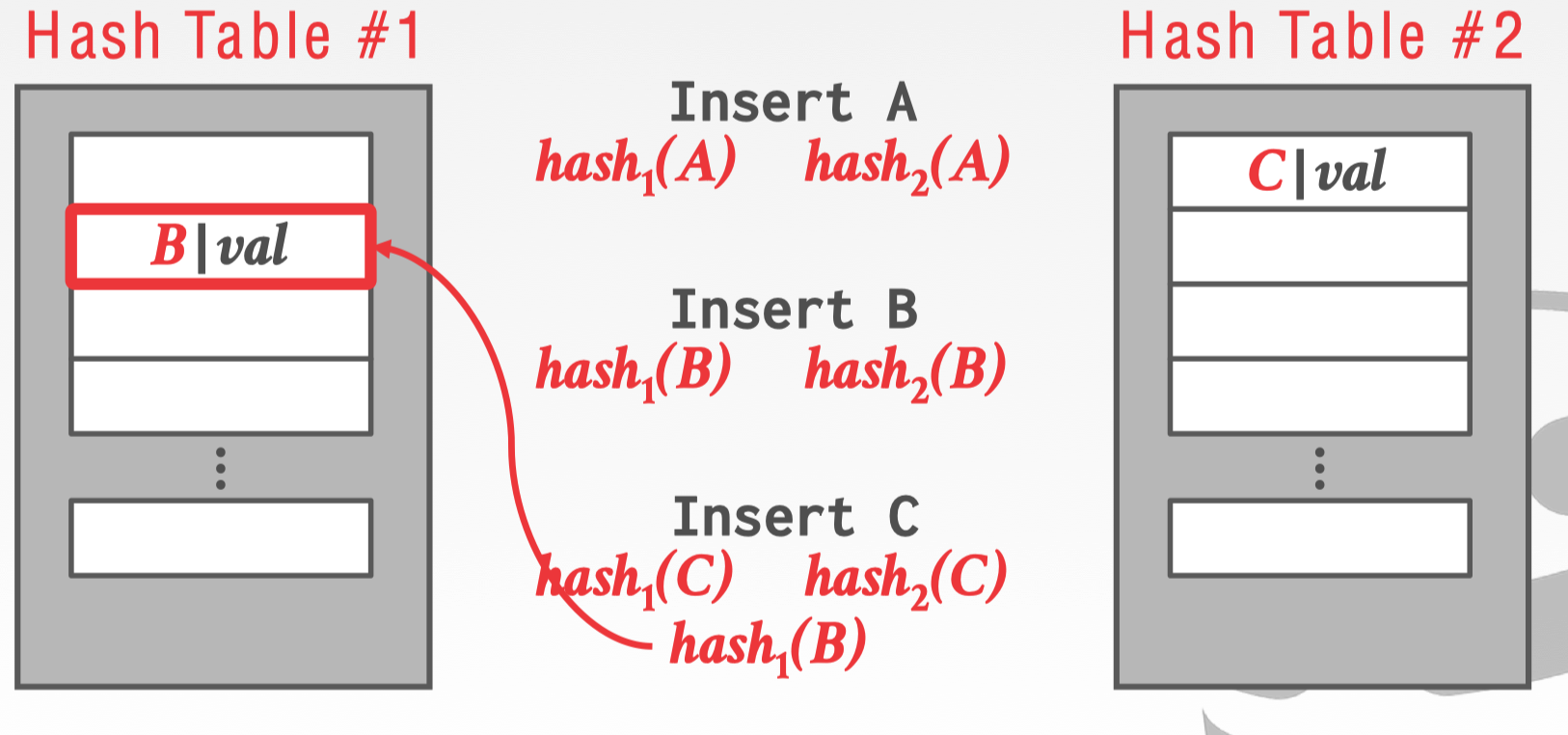
image-20230510090645914

逐出之后，使用 hash1 重新 hash 到另个 table 中，这个位置也不是一个空的 slot，B 把 A 的位置再次占用，A 又被逐出。

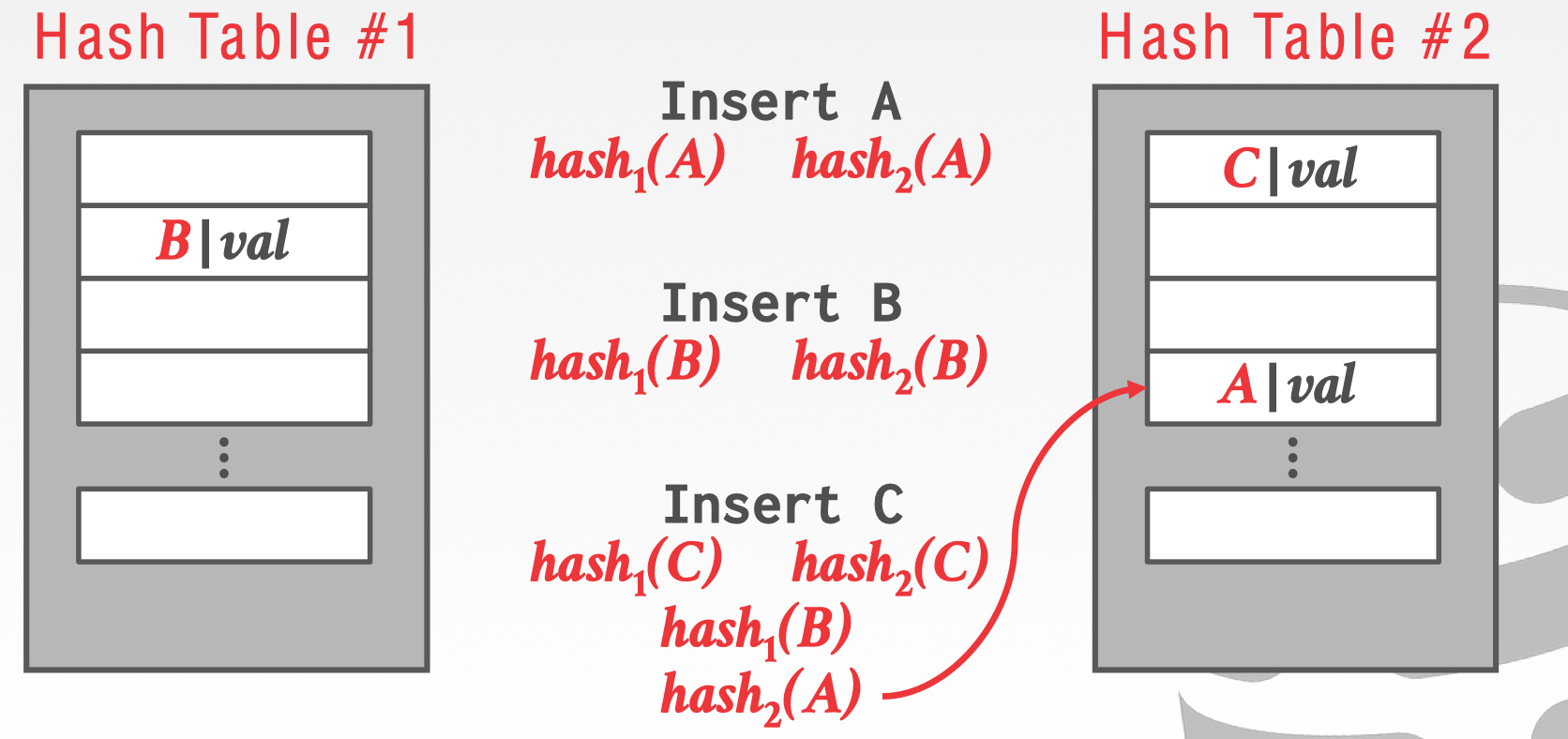
image-20230510090806485

再次使用另个 Hash Table 的 hash2，找到有一个空的 slot 可以插入，此时 A 就存在另一个 Hash Table 中。

Dynamic Hashing Schemes

静态的 Hash Table 总是需要提前预知大致的数据量，如果用超了需要购进新的 Hash Table 来扩容或者缩容，就会涉及的数据的移动。

动态的 Hash Table 可以根据需要自动调整大小：

  • Chained Hashing
  • Extendible Hashing
  • Linear Hasing

Chained Hasing

每个 slot 包含 buckets 的链表的 hash table，把相同 hash key 的元素放入同一 bucket 中来解决冲突。

  • 要确定元素是否存在，需要找到特定的 bucket 进行 scan
  • 插入和删除本质与查询一致

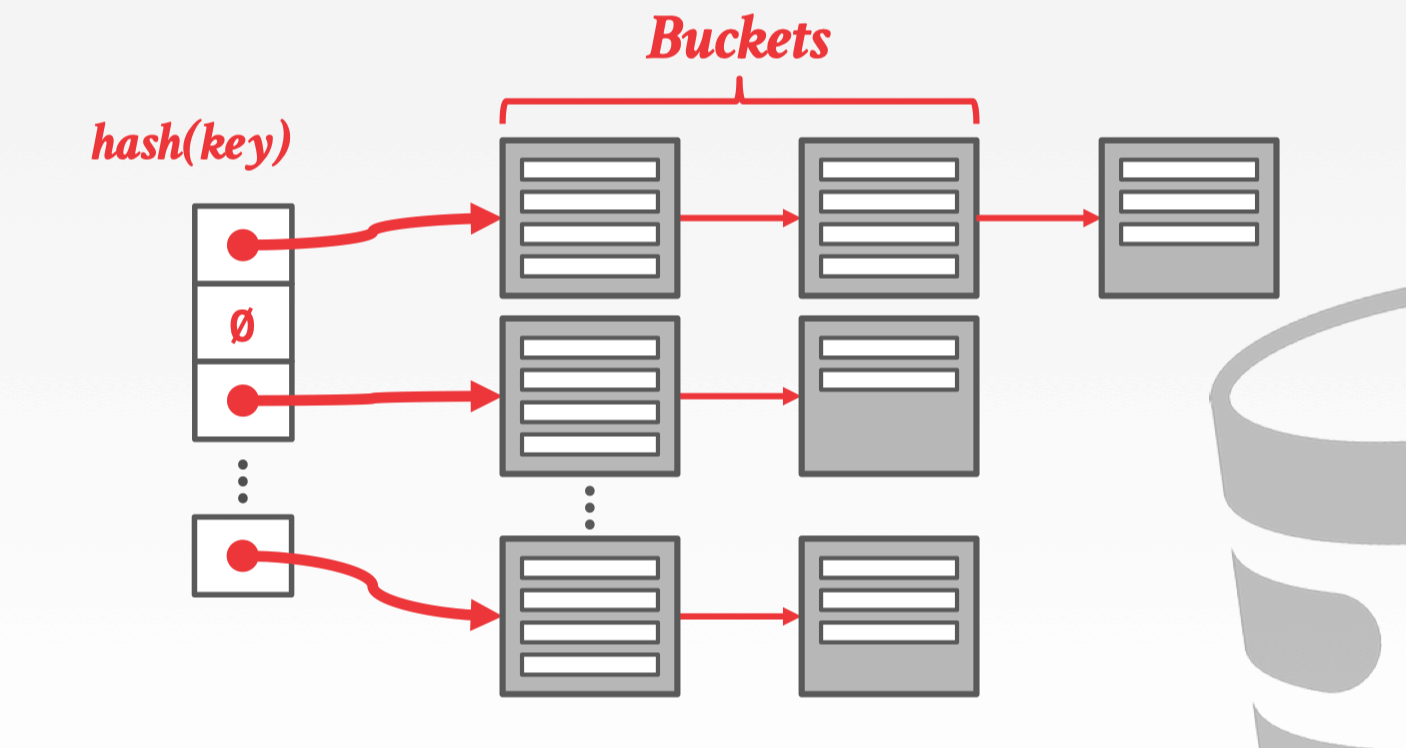
Extendible Hashing

Chained Hasing 的方案明显的缺点就是一个 linked list 可能会无限增长，而 Extendible Hasing 不但可以让多个 slot 对应相同的 bucket chain，而且在面对 bucket 溢出的时候，可以只针对这个 bucket 做拆分，只移动少量的数据。

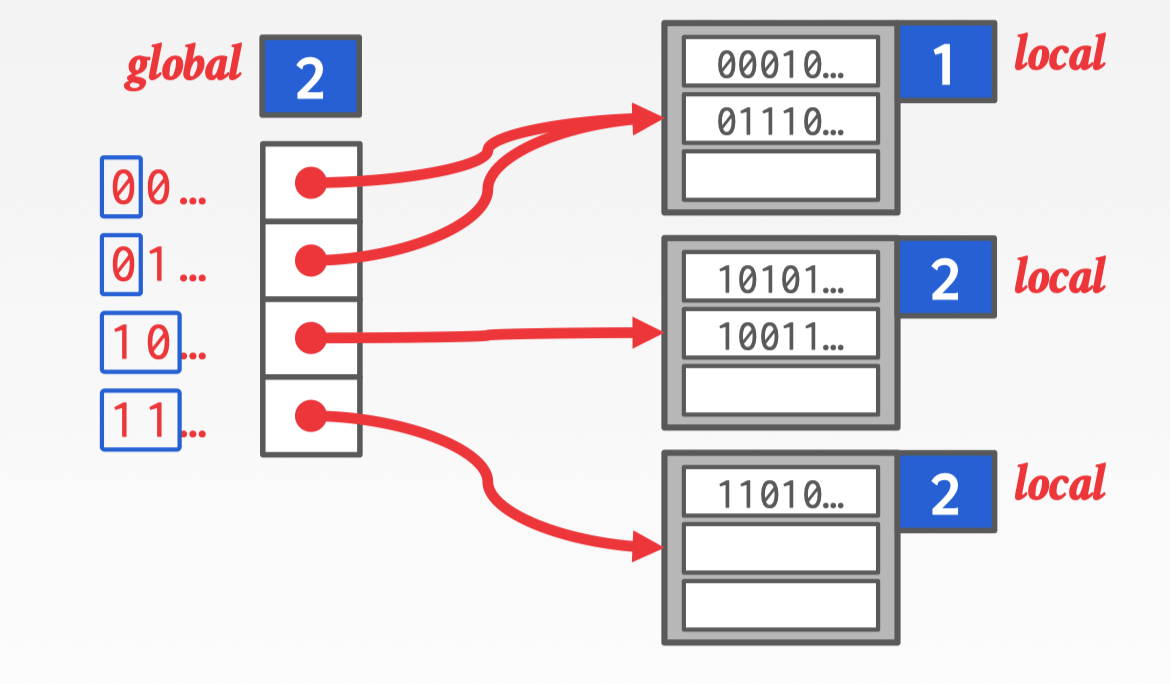
  • slot Array：数组中存储者指向 bucket 的指针，有一个 global count 用作判断前 n 位与 bucket 的对应关系
  • Bucket：存储的单元，有 local count，表示使用 n 位可以定位该 bucket

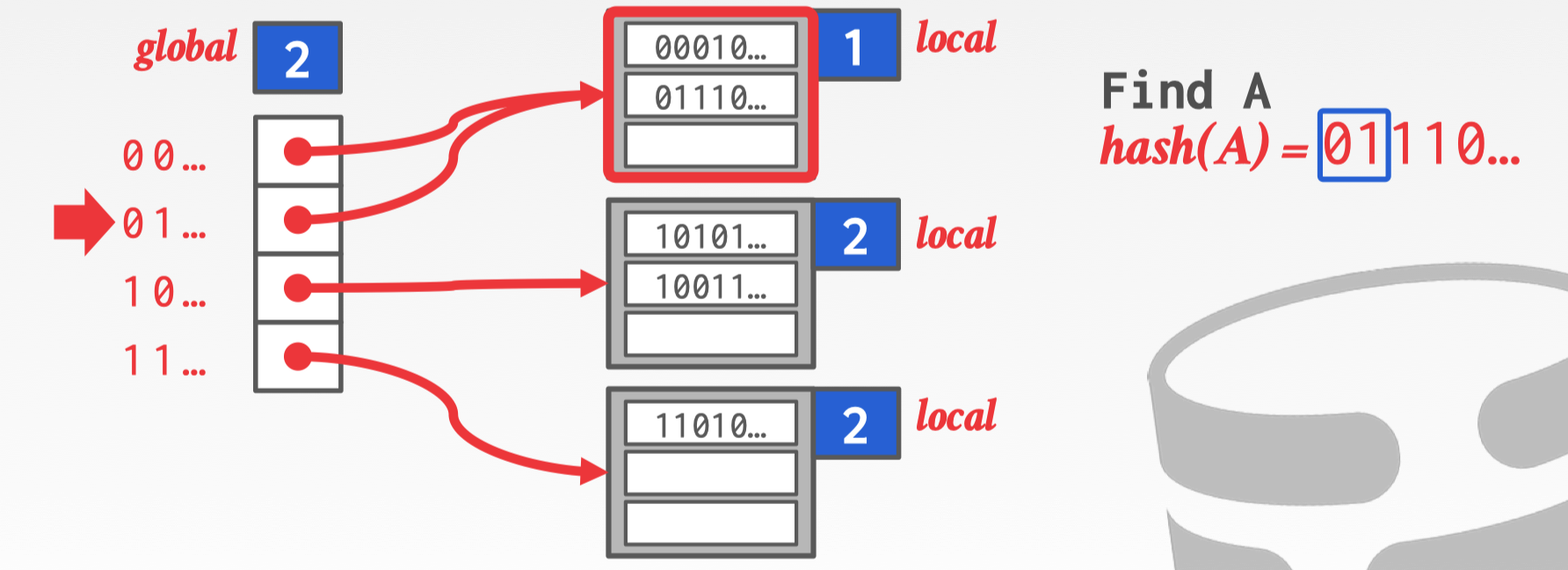
image-20230517085037001

Hash(A) = 01110… 根据 global count 判断前 2 位是 01 所以指向了第一个 bucket，在 bucket 中扫描找出 A。

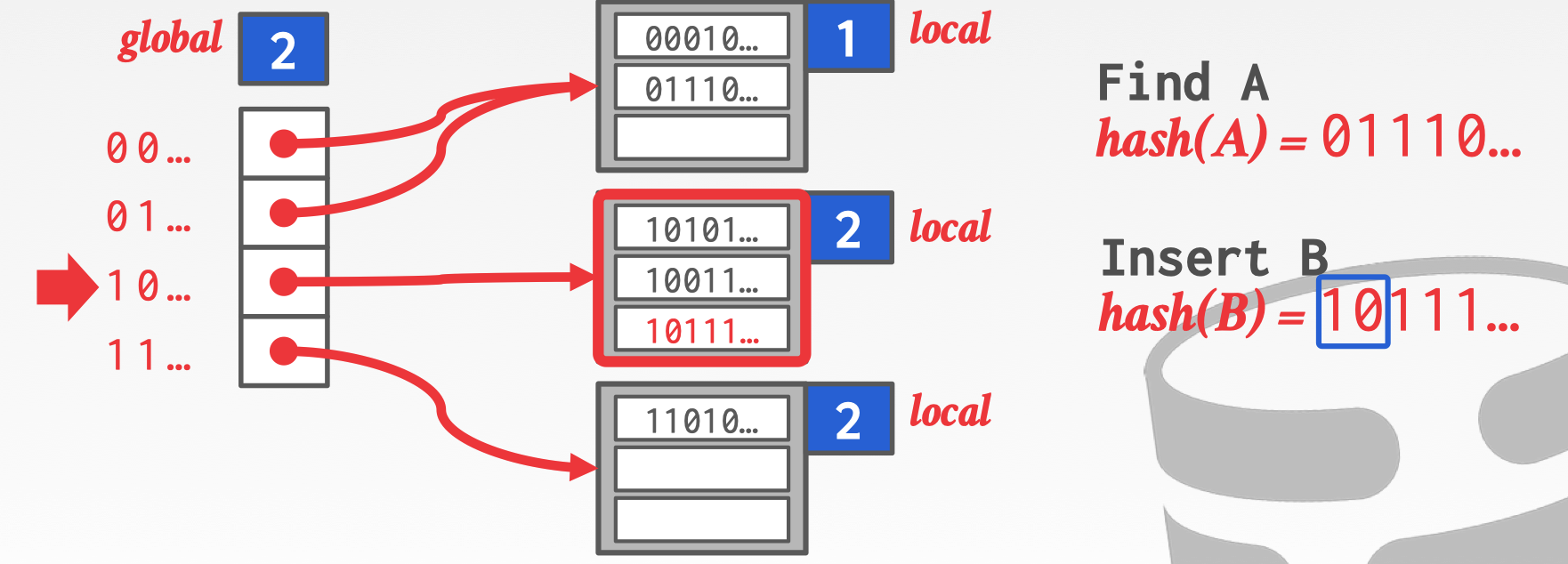
image-20230517085441826

同理 B 通过前两位判断出处于第二个 bucket 中，然后插入到最后。

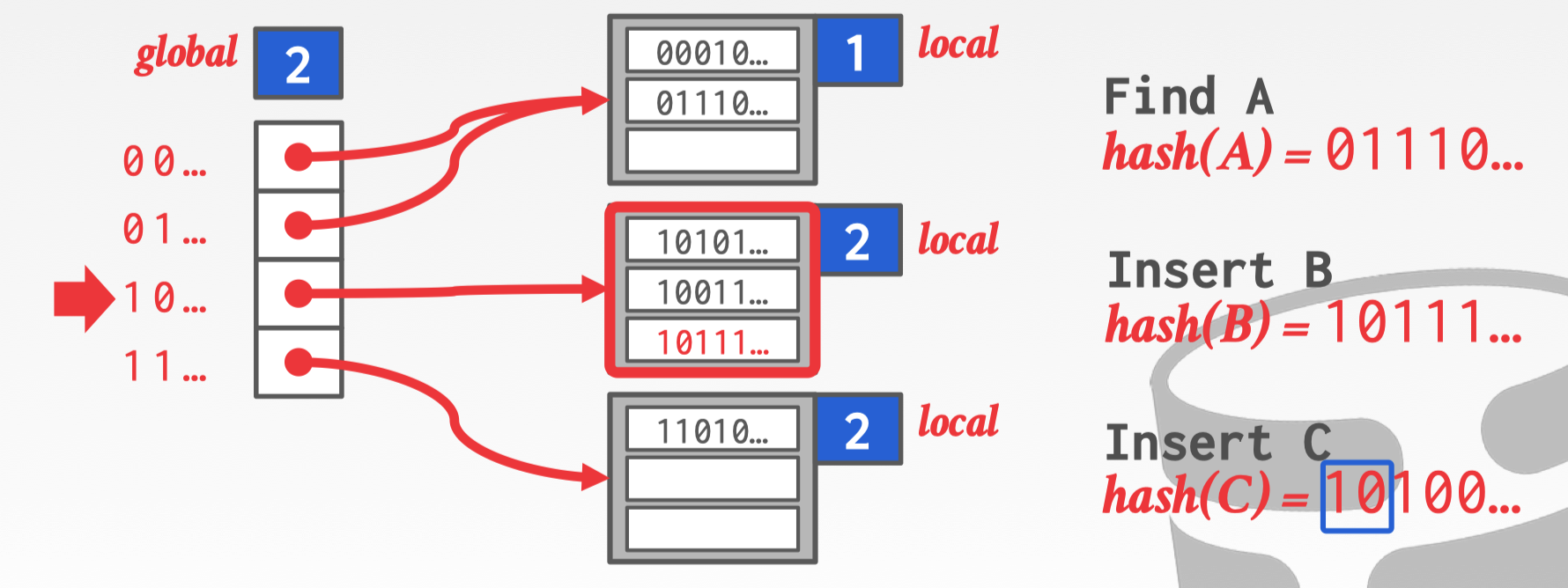
image-20230517085609379

此时要插入 C，通过 Hash(C) 发现应该插入第二个 bucket，但是此时 bucket 已经满了无法插入，需要扩容。

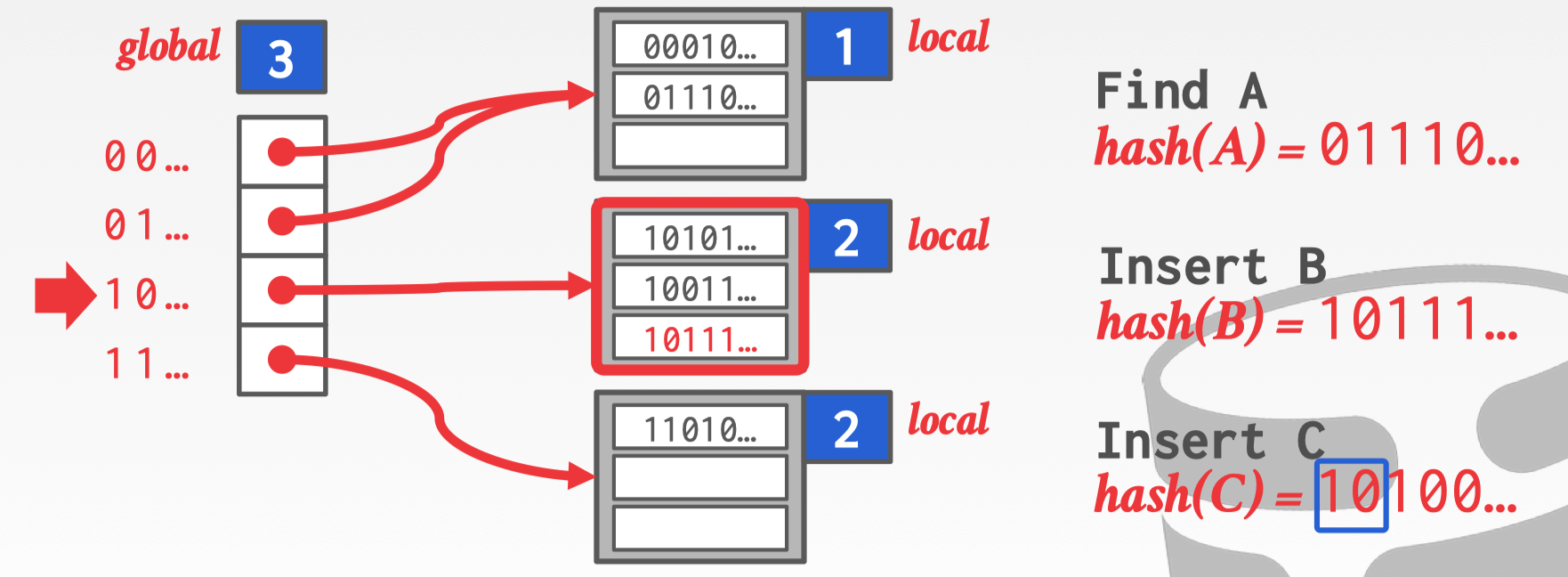
image-20230517085712999

第一步提升 global count 为 3。

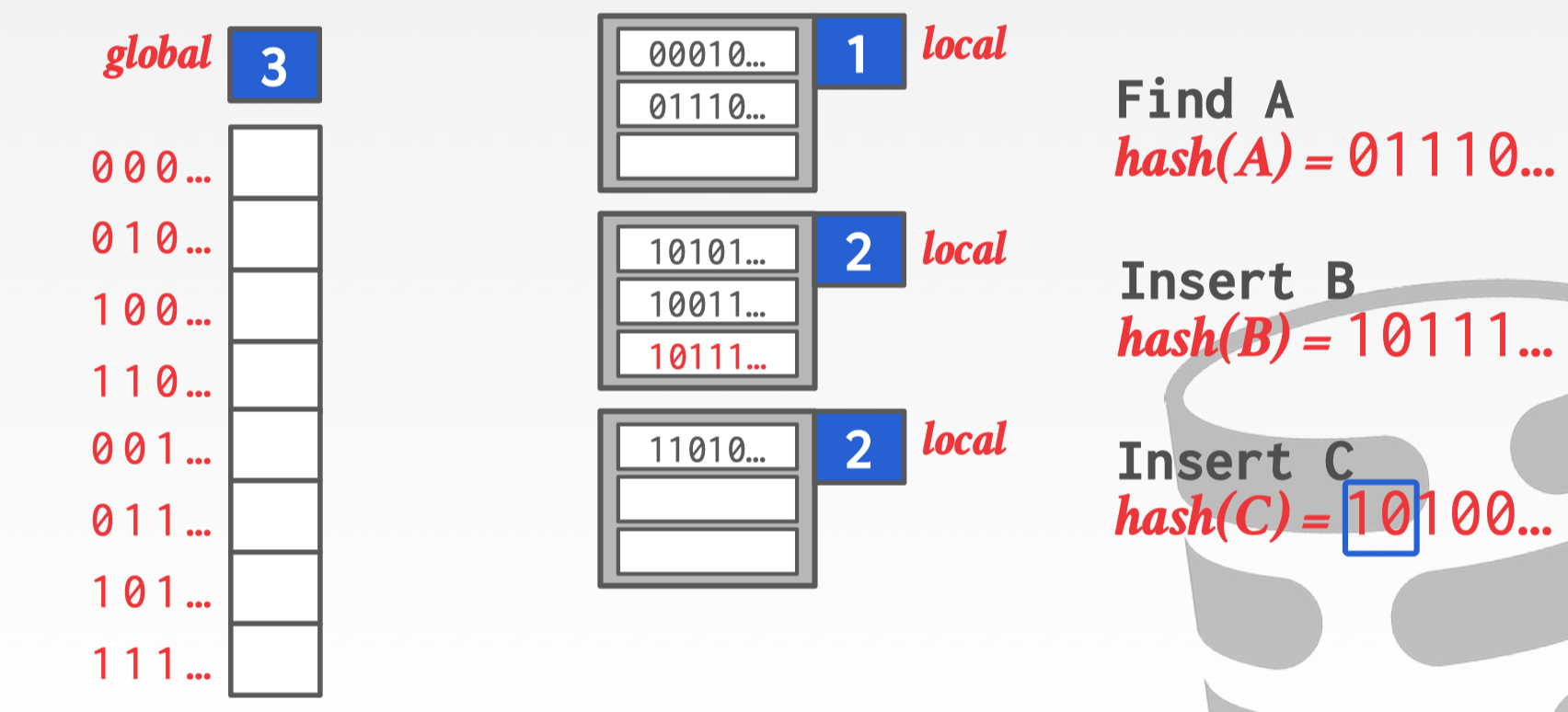
image-20230517085742687

第二步根据 global count 重新生成 slot array，这步并不会由太大影响 slot array 本身只存储着一些指向 bucket 的指针，只需要加上 latch 后扩容重新写入这个过程很快。

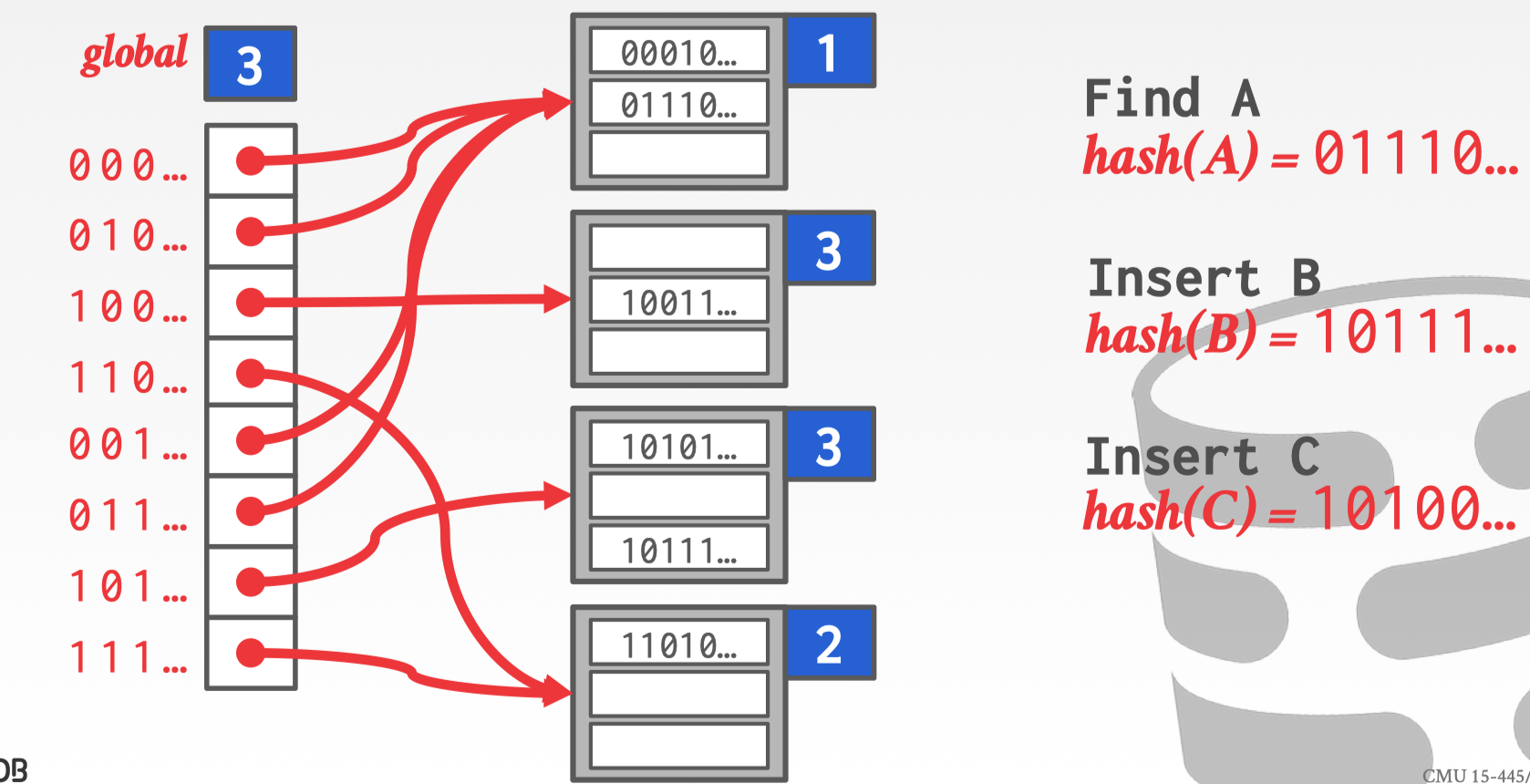
image-20230517085936729

第三步，拆封那个将要溢出的 bucket，提升它们的 local count 为3，重新映射 slot 与 bucket 的关系。这里拆分只是那个溢出的 bucket 其他的数据不动，所以这个过程也是很快。

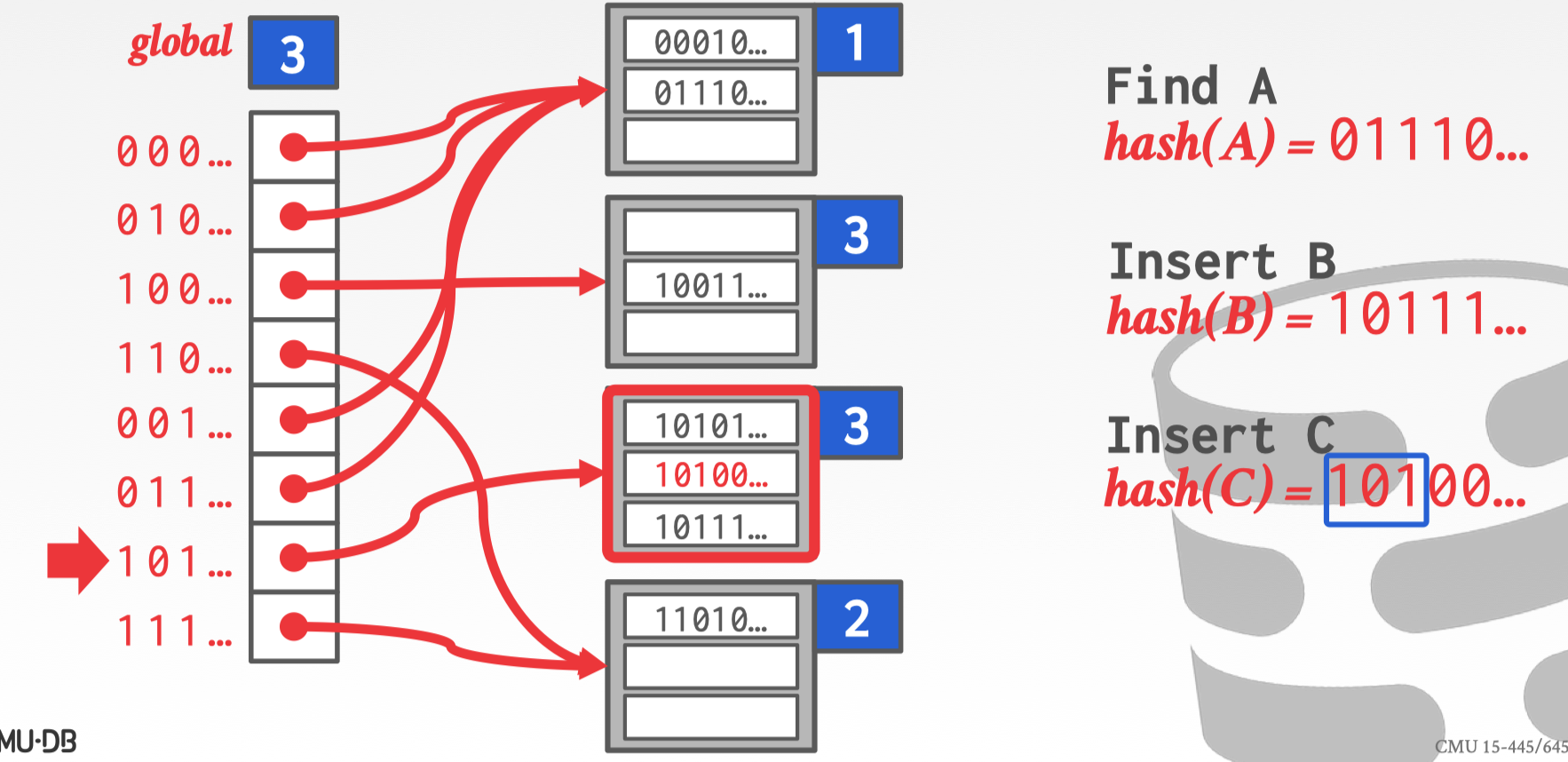
最后插入 C 到拆分后的第三个 bucket。

Linear Hasing

Extendible Hasing 虽然很好解决了无限插入的问题，但是在扩容时候需要对 slot array 加 latch 扩容，这就会导致些阻塞，如果 bucket 不断地 overflowed 就会影响性能。

Linear Hasing 在 Extendible Hasing 的基础上进一步解决了这个问题，但是带来了更复杂的操作。

  • split pointer：指向下一个要被拆分的 bucket，当任何一个 bucket overflow，就拆分指向的 bucket，与 overflow 的 bucket 无关
  • multiple hash function：被 split 的 bucket 需要使用另一个 hash 函数来定位新的位置

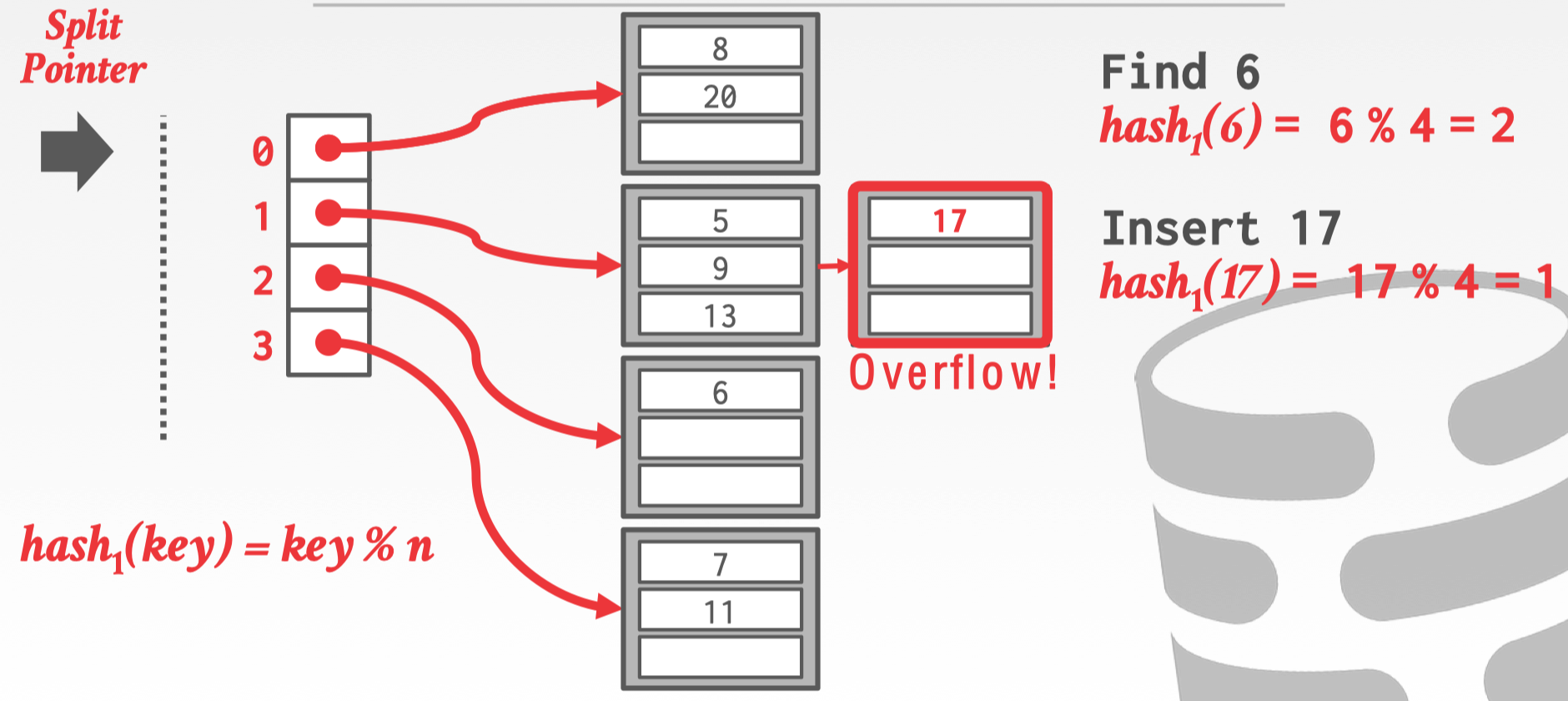
image-20230517092212146

假如要插入 17，第一个 hash 发现要插入 slot 位 1 的 bucket，但是 bucket 发生了 overflow，采取 chained hasing 的做法，加入一个 linked bucket，存储 17，此时 split point 指向的是 slot 为 0 的 bucket，所以要对这个 bucket 拆分。

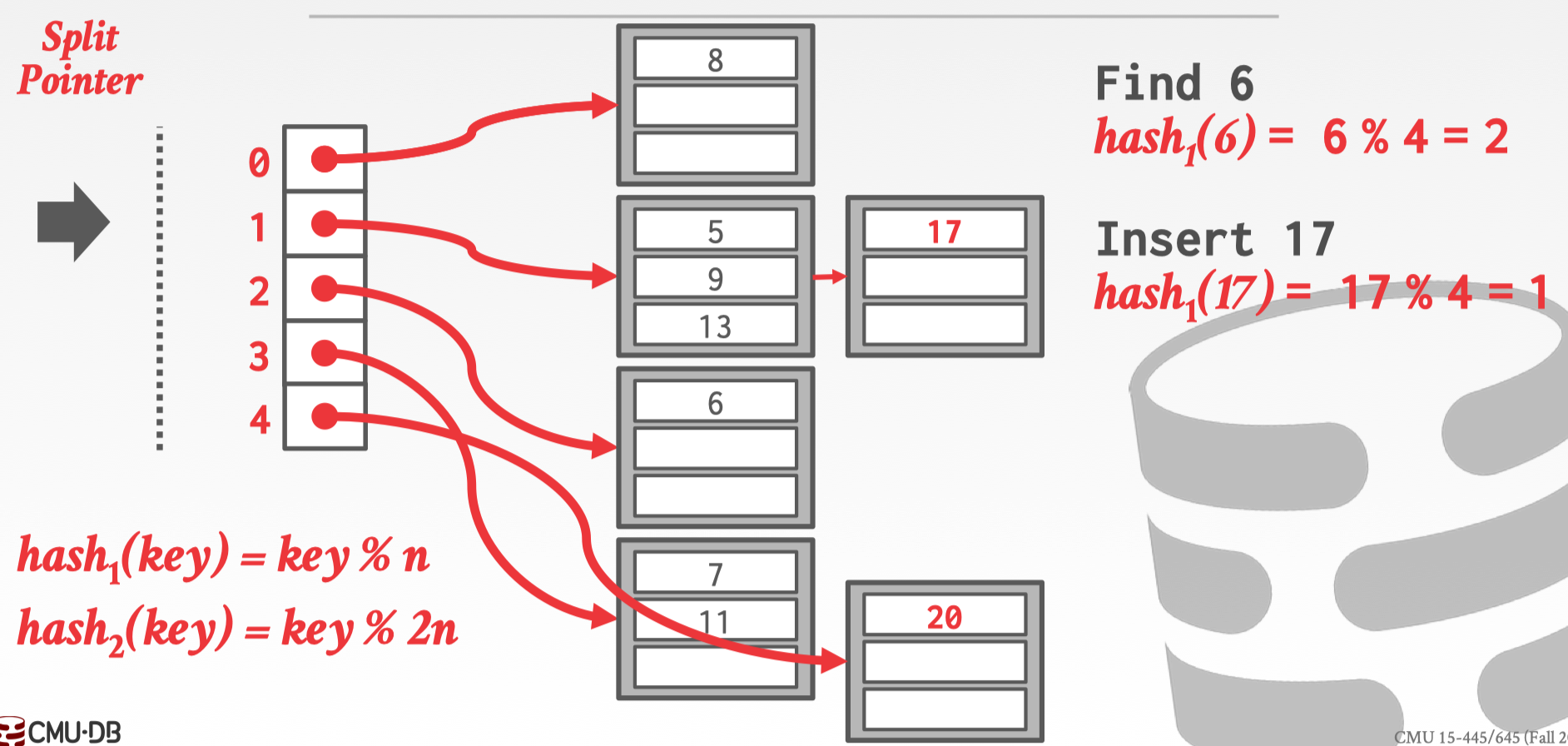
image-20230517092417589

拆分 slot 为 0 的 bucket，需要移动该 bucket 中的数据到新的 bucket 中，然后 split point 向下移动此时指向的是 slot 为 1 的位置。

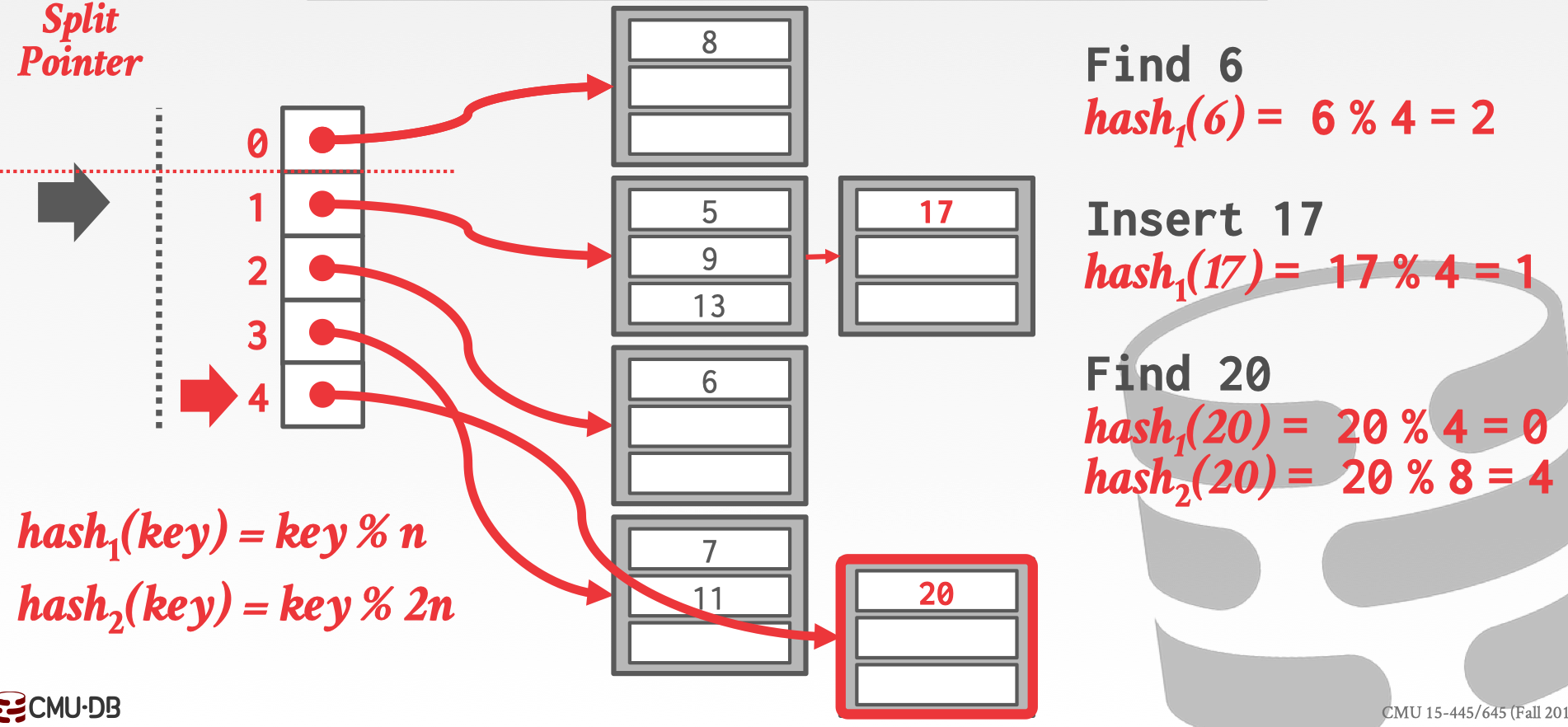
image-20230517092745162

加入此时需要 Find 20，经过第一个 hash 后发现是处于 split point 之前的 slot，所以需要进行二次 hash，找到 slot 为 4 的位置，20 就存在该 bucket 中。

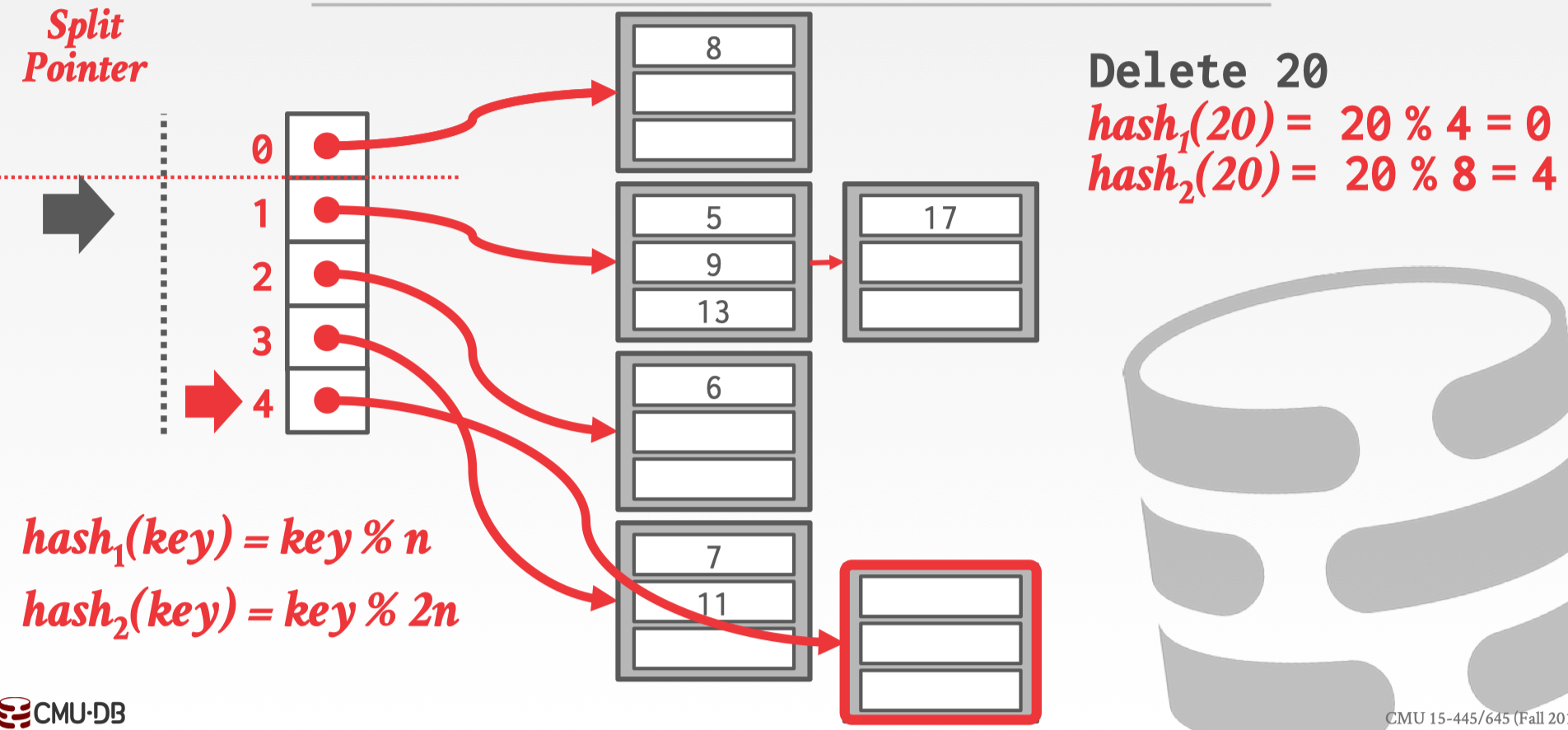
image-20230517093359425

插入时候需要考虑扩容问题，那么删除的时候也需要缩容问题，假如此时删除 20，经过上面描述的方法两次之后找到了 20 位于 slot 为 4 的 bucket 中，并把 20 删除，此时该 bucket 为空。

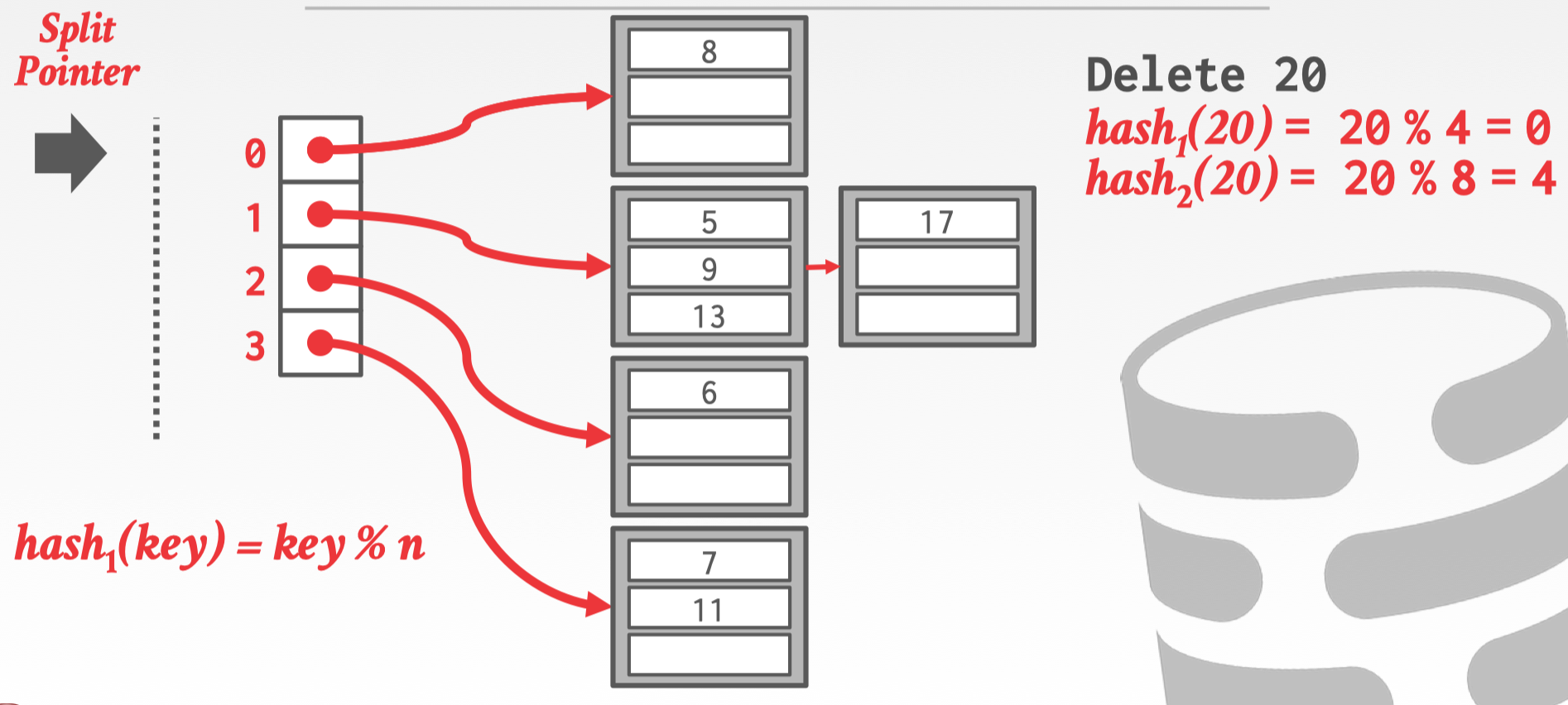
image-20230517093609074

删除该 bucket 与 slot，同时要把 split pointer 往回移动，同时删除第二个 hash 函数，相反地如果 split pointer 走完了一轮 slot array 那就重新来过删除第一个 hash 函数，生成第三个 hash 函数。

总结

Hash 可以在 O(1) 的时间复杂度内快速地查找，但是缺点就是只能对精确的 key 查找，无法根据一些条件来模糊查找。